 物理学
物理学 二重スリット実験とシュレディンガー方程式
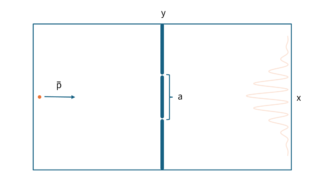
二重スリット実験に関するシュレディンガー方程式の解を導出する。二重スリット実験のような現象が相対論的な時空の性質に原因があるという仮説を合わせて提示する。
 物理学
物理学  物理学
物理学  物理学
物理学  物理学
物理学  物理学
物理学  物理学
物理学  物理学
物理学  物理学
物理学  物理学
物理学  物理学
物理学