 解析学
解析学 正則関数の微分
複素関数(正則関数)の微分について簡単に記述する。教科書的な内容であり退屈かもしれないが、実関数の微分との差異が分かりやすいように書いてみた。
 解析学
解析学  物理学
物理学  代数学
代数学  解析学
解析学  解析学
解析学 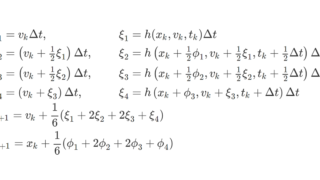 解析学
解析学  物理学
物理学 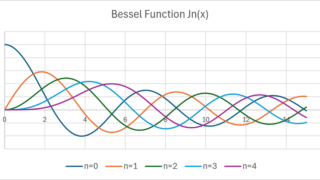 解析学
解析学  物理学
物理学