概要
テキサスホールデムには、他のプレイヤーから獲得したチップがそのまま勝ち分になるリングゲームとプレイヤー間でどれだけ長く生き残れるかの順位を競い、その順位に応じて賞金を受け取るトーナメントの二形態がある。リングゲームではチップの期待値を最大化するようにプレイをすればよい(筆者はこの考え方に疑問を抱いているけど)のであるが、トーナメントでは順位を競った結果受け取れる賞金の期待値を最大化する必要がある。これを計算するには、現在のプレイヤーにおけるスタックの分布からどの順位にランクインできるかの確率を計算する必要がある。これを推定するモデルについて紹介しようというのが本稿の内容である。
ICM (Independent Chip Model)
\(\small n\)人のプレイヤーがスタックを\(\small s_1,\cdots,s_n\)ずつ持っていると仮定する。このとき、プレイヤー\(\small i\)が優勝する確率が現在のスタックに比例するものと仮定する。順位が1位であるプレイヤーが\(\small i\)であることを\(\small r_1 = 1\)と表すと、プレイヤー\(\small i\)が優勝する確率は
\[ \small p_i^{(1)} = \text{Pr}[r_1=i] = \frac{s_i}{\sum_{z=1}^n s_z} \]
と表現できる。さらに、1位のプレイヤーが\(\small i\)であるときに、2位のプレイヤーが\(\small j\)である確率が\(\small i\)のスタックを除いたスタックに比例すると仮定し、
\[ \small p_{ij}^{(2)} = \text{Pr}[r_2 = j \:|\:r_1=i] = \frac{s_j}{\sum_{z=1,z\neq i}^n s_z} \]
で与えられると仮定する。この場合、1位のプレイヤーが誰であるかにかかわらず、2位のプレイヤーが\(\small j\)である確率は
\[ \small p_j^{(2)} = \sum_{i=1, i\neq j}^n p_{ij}^{(2)} \]
で計算できることは理解できるだろう。
同様にして3位以降の確率も計算できる。1位のプレイヤーが\(\small i\)、2位のプレイヤーが\(\small j\)であるときに、3位のプレイヤーが\(\small k\)である確率が
\[ \small p_{ijk}^{(3)} = \text{Pr}[r_3 = k \:|\:r_1=i,r_2=j] = \frac{s_j}{\sum_{z=1,z\neq i,j}^n s_z} \]
で与えられると仮定する。この場合、1位、2位のプレイヤーが誰であるかにかかわらず、3位のプレイヤーが\(\small k\)である確率は
\[ \small p_k^{(3)} = \sum_{i=1, i\neq k}^n \sum_{j=1, j\neq i,k}^n p_{ijk}^{(3)} \]
と計算できる。これを繰り返せば、スタック\(\small s\)を持っているプレイヤーが何位になるかの確率をすべて決定することができることになる。
このような計算でプレイヤーが何位になるかの確率を計算する方法はICM(Independent Chip Model)と言われる。上記の計算では暗黙的に、二人のプレイヤーの順位が\(\small i<j\)となる確率は、別のプレイヤー\(\small k\)の存在に影響を受けないということを仮定している。このような仮定は意思決定理論ではIIA(Independence from Irrelevant Alternatives、無関係な選択肢の独立性)という。この仮定はしばしば競馬や競艇など順位に賭けるギャンブルの勝利確率の推定に用いられることもある。経済学では社会選択理論など投票による選択肢の順位を決定する際にも、この条件を仮定することが少なくない(批判も少なくないけど)。
重要な注意点として、上記の計算式の構造を見ればわかるように、この計算の計算量はプレイヤーの人数\(\small n\)が増加するにつれて指数関数的に増加することになる。そのため、厳密な計算ができるのは\(\small n\)が小さいときのみであり、\(\small n\)が大きい場合はモンテカルロシミュレーションで概算値を計算するしかないだろう。モンテカルロシミュレーションで計算する方法については後述する。
トーナメントにおける賞金のモデル
ICMは稼いだチップの量ではなく、プレイヤー間の順位が獲得できる賞金に紐づくトーナメントにおける目的関数として用いられる。そのため、トーナメントが各順位にどの程度の賞金を割り当てているかが重要になる。これは一般的にべき関数に従って大体決定される傾向がある。これは以前のパレートの法則の投稿
で述べたものである。労働者の所得がべき関数に近い形状で決定されていると述べたが、トーナメントの賞金もそれと類似の方法に従って決定されるということである。おそらく、このような方法で報酬を決定することが多くの人々の意欲を掻き立てるために役に立つためだろう。ビジネスパーソンもポーカープレイヤーも胴元にインセンティブを付けられて良いように利用されているという意味では同類でしかないのかもしれない。
簡単な例を用いて具体的な計算方法を示してみよう。参加者が100人のトーナメントで一人当たり参加料を100ドル支払うものとする。合計の賭け金が10000ドルであり、カジノの手数料(テラ銭)として10%の1000ドルを差し引いた9000ドルを賞金として配分するものとする。賞金を受け取れるプレイヤーは上位10%の10人であると仮定し、その合計額が9000ドルになるように各順位の賞金を定めよう。
優勝者が受け取ることができる賞金を\(\small W_1\)として、2位以降の賞金額を
\[ \small W_m = \frac{W_1}{\beta^{m-1}}, \quad \beta>1 \]
と定めることにする。このとき、合計の賞金額は
\[ \small W = \sum_{m=1}^{10} W_m = 9000 \]
となるように\(\small W_1\)と\(\small \beta\)の値を定めれば良い。このとき、10位入賞者が獲得する賞金が参加料を上回る範囲で\(\small \beta\)を定めれば良いだろう。\(\small \beta\)の上限値は1.45ぐらいであるが、ここでは\(\small \beta=1.35\)と置いて各順位の賞金額を計算してみよう。具体的には以下のように計算できる。
| 順位 | 1/β^(m-1) | 賞金 |
|---|---|---|
| 1 | 1 | 2455 |
| 2 | 0.74074 | 1819 |
| 3 | 0.54870 | 1347 |
| 4 | 0.40644 | 998 |
| 5 | 0.30107 | 739 |
| 6 | 0.22301 | 548 |
| 7 | 0.16520 | 406 |
| 8 | 0.12237 | 300 |
| 9 | 0.09064 | 223 |
| 10 | 0.06714 | 165 |
ICMから計算したプレイヤー\(\small i\)の順位が\(\small m\)位になる確率と\(\small m\)位になった時に受け取れる賞金額\(\small W_m\)からプレイヤー\(\small i\)が受け取ることができる賞金額の期待値\(\small R_i\)は
\[ \small R_i(s) = \sum_{m=1}^{10} p_i^{(m)}(s) W_m \]
と計算できる。\(\small s\)はすべてのプレイヤーのスタックのベクトルである。トーナメントでは、スタックの期待値を最大化する代わりにこの\(\small R_i(s)\)を最大化するようにベット戦略を考えていく必要があるということになる。
モンテカルロシミュレーションによる推定
ICMの厳密な計算は参加人数\(\small n\)に対して計算量が指数関数的に増加するが、モンテカルロシミュレーションを用いれば容易に計算できる(シミュレーション誤差は生じるけど)。単純に、スタックから計算した確率分布から1位のプレイヤーを乱数で選出、1位のプレイヤーを除いた確率分布から2位のプレイヤーを乱数で選出、・・・を繰り返せば容易に各プレイヤーが何位になるかの確率分布を推定できることは理解できるだろう。pythonで実装したソースコードを掲載しておく。なお、ソースコードはChatGPTに書かせた模様・・・
import random
def calc_icm(stack, n_simulation):
n = len(stack)
r = [[0 for _ in range(n)] for _ in range(n)]
# 正規化された確率ベクトル
total = sum(stack)
p = [s / total for s in stack]
for _ in range(n_simulation):
ranking = []
q = [0] * n
for _ in range(n):
# 残っているプレイヤーの合計確率を計算
remaining_indices = [k for k in range(n) if k not in ranking]
remaining_total = sum(p[k] for k in remaining_indices)
# qを更新(現在選ばれる確率)
for k in range(n):
q[k] = p[k] / remaining_total if k in remaining_indices else 0.0
# ランダムに1人を選出
v = random.random()
acc = 0
for k in range(n):
acc += q[k]
if v <= acc and q[k] > 0:
ranking.append(k)
break
# ランキングの結果をrに加算
for position, player in enumerate(ranking):
r[player][position] += 1
# 平均化
for i in range(n):
for j in range(n):
r[i][j] /= n_simulation
return r
if __name__ == "__main__":
# 例: プレイヤーが4人いて、それぞれのスタック量が以下の通り
stack = [1000, 1500, 2000, 500]
# シミュレーション回数(大きいほど精度が上がります)
n_simulation = 10000
# ICM計算を実行
icm_result = calc_icm(stack, n_simulation)
# 結果の表示
print("ICM確率分布(行:プレイヤー、列:順位)")
for i, row in enumerate(icm_result):
print(f"プレイヤー{i+1}: " + " ".join(f"{prob:.4f}" for prob in row))具体的なイメージを理解するため、10人のプレイヤーが残っており、それぞれのスタックが
\[ \small s = \{s_1,\cdots,s_{10}\} = \{18,16,14,12,11,9,8,6,4,2\} \]
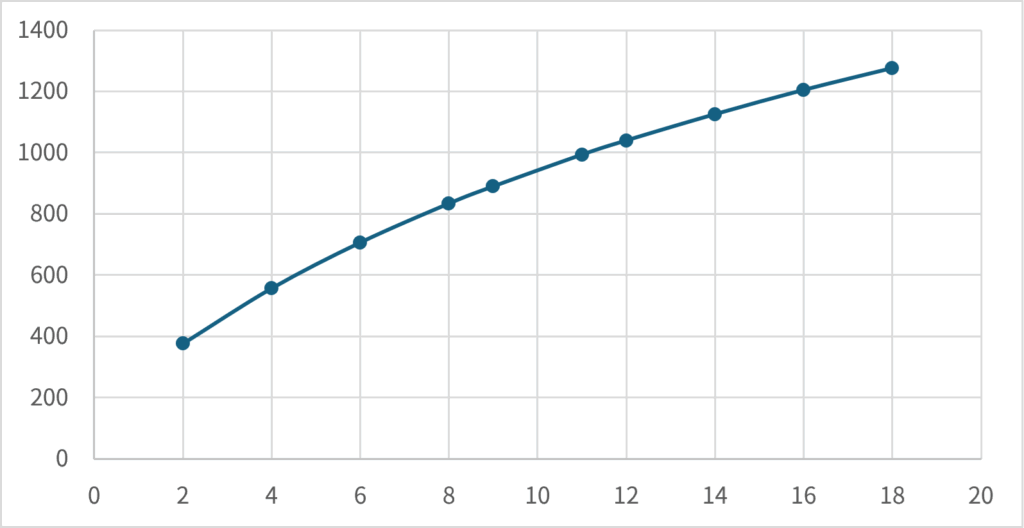
であるとする。このときの各プレイヤーの期待賞金額\(\small R_i(s)\)を求めてみよう。これをスタック順に並べれば、スタックに対する期待賞金額の関数\(\small R(s)\)の形状を求めることができるだろう。ICMで推定した各プレイヤーがどの順位になるかの確率は以下の通りである。
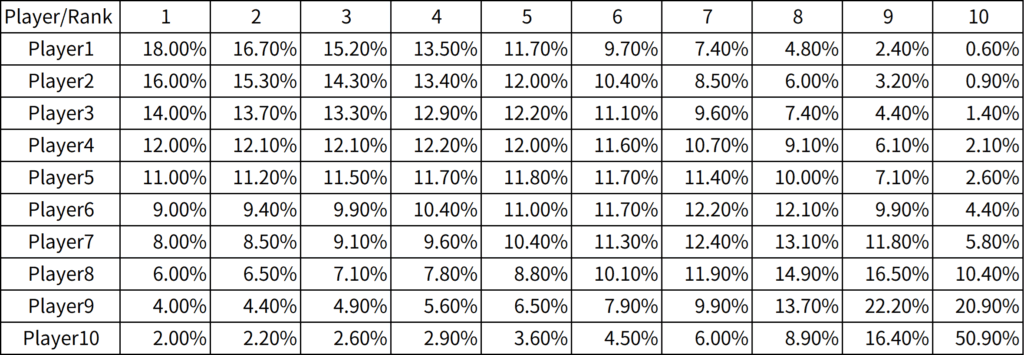
1位から10位の賞金額が前節の表で与えられると仮定する。各プレイヤーの期待賞金額\(\small R_i(s)\)を計算して、スタック\(\small s\)についてプロットすると以下の通りである。
べき乗効用関数(CRRA型効用関数)
前節のグラフを見ると、期待賞金額がスタック\(\small s\)について上に凸関数になっていることが見て取れるだろう。言い換えれば、期待賞金額をスタック\(\small s\)に関する効用関数と考えるならば、スタック\(\small s\)についてリスク回避的な行動をとることが最適になると推測できる。また、グラフの形状からCRRA型効用関数
\[ \small U(s) = \frac{s^{1-\gamma}-1}{1-\gamma} \]
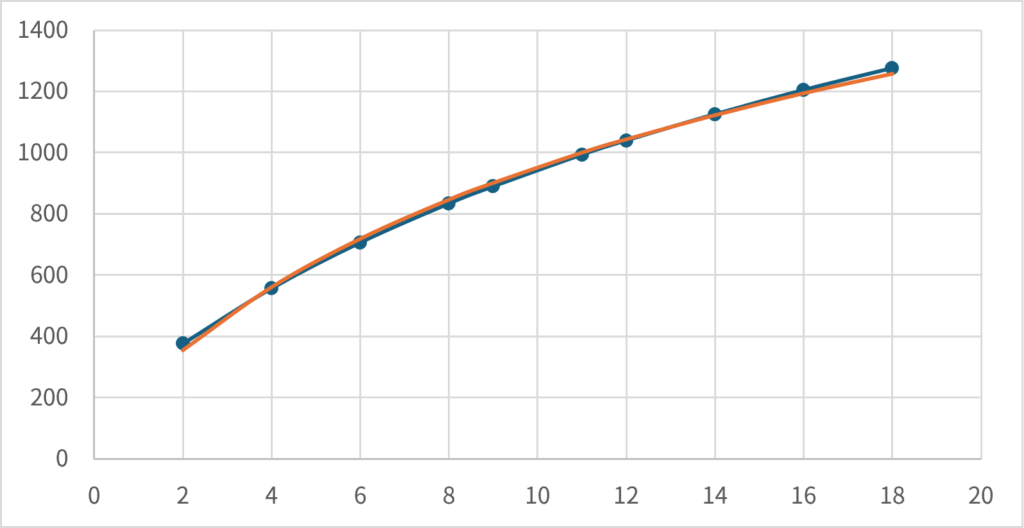
において、\(\small \gamma < 1\)と置いた場合の関数の形状に類似していることが見て取れる。CRRA型効用関数で\(\small \gamma < 1\)である効用関数はべき乗効用関数と言われる。この場合\(\small s=0\)であっても、\(\small U(s)\)は有限の値として計算できるため、テキサスホールデムのようにスタックが0になる可能性があるゲームでもリスク回避を表現する効用関数として用いることができる。
実際に、前節のグラフを\(\small \gamma = 0.25\)と置いた関数を用いて近似すると大体一致していることが見て取れるだろう(\(\small 1/1.35 \approx 0.74 \approx 1-\gamma\)で推測したが、プレイヤーの数が増えるにつれて\(\small \gamma\)は小さく設定する必要がある)。オレンジ色の線はべき乗効用関数を\(\small U(s) = s^{1-0.25}\)と置いて、\(\small R(s) = a + b U(s)\)で二乗誤差が最小になるように\(\small a,b\)を定めた(線形変換した)値をグラフにしたものである。
教科書的なテキサスホールデムの戦略の多くはスタックの期待値を最大化するように計算されている(\(\small \gamma=0\))ため、トーナメントの上位争いで用いるにはリスクを取りすぎているということになるだろう。プリフロップにおけるハンドレンジの選び方やベット戦略について、このリスク回避度に応じた調整を入れる必要があるということになる。もちろん、残っているプレイヤーが多くほとんどのプレイヤーが賞金を獲得できない状況ではこのような計算は不要であり、スタックの期待値を最大化するようにプレイすればよい。一方で、上位入賞が見えてきた場合は多少リスク回避的に手札を選択したり、(ショートスタックでも安易に中途半端な手札でプリフロップオールインしないなど)ベット額を調整することで1ゲームでも多く生き残り、より上位の順位に入賞できるようにプレイする必要があるということだろう。



