概要
シュレディンガー方程式における二重スリット実験の取り扱いについて説明する。二重スリット実験については、数式を使わない説明が無数に存在するが、数式を使ってシュレディンガー方程式における二重スリット実験の計算を説明した文章というのを見たことがあるだろうか?もちろん、これもいくばくかは存在するが、間違っている計算をしている論文やサイトも少なくなく、適切な計算で導出している説明を発見することがなかなかに困難であったりする。
実を言うと、筆者は量子力学を調査する初期の段階で、シュレディンガー方程式の解を知りたくて二重スリット実験の解を探したところ、なかなか発見できなくて苦労した。イライラしながらgoogleで検索しまくった結果、英語の掲示板サイトで、”シュレディンガー方程式で二重スリット実験の干渉縞の計算はどうやって導出すればよいのか?”という質問が出ているのを発見して、それを自分も知りたいと思った。回答はTomonagaの”Quantum Mechanics, Vol 2.”に載っているよというものであった。英語だったし、回答者も日本人ではないようだったので、みんな苦労しているのではないかと思った次第である。
無事日本語版の朝永振一郎の”量子力学Ⅱ”を入手して計算結果を確認することができた。もともとブラウン運動の理論で量子力学を定式化してみようと考えて調査を始めたのであるが、その計算結果から量子の運動をブラウン運動で記述することは無理そうだということを理解したというのが筆者の量子力学の調査のスタート地点であった。ということでこれを紹介するのがこの記事の趣旨である。また、筆者の書籍で紹介している二重スリット実験の解釈についても最後に簡単に紹介しようと思う。
二重スリット実験の概要
検「その部屋には二つの窓が前庭に向いて並んでいる。被告はそのどちらの窓から侵入したのか。この点は非常に重要なことだから、はっきりと答弁してほしい」
これに対する被告の答は、はなはだ奇想天外なものでありました。
被「私は二つの窓の両方を一緒に通って室内に入ったのです」
朝永振一郎、”光子の裁判”
二重スリット実験は物理学の中でも最も美しい実験の一つであると言われる。そう言われるだけあり、実験の内容自体は非常にシンプルである。しかし、その結果は多くの困惑をもたらす実験になっている。電子や光子を二つの穴(スリット)が開いた空間に発射すると、1回1回は粒子であるかのように検出される。一方で、これを複数回繰り返すと以下のような波打ったような確率分布として検出されることになる。
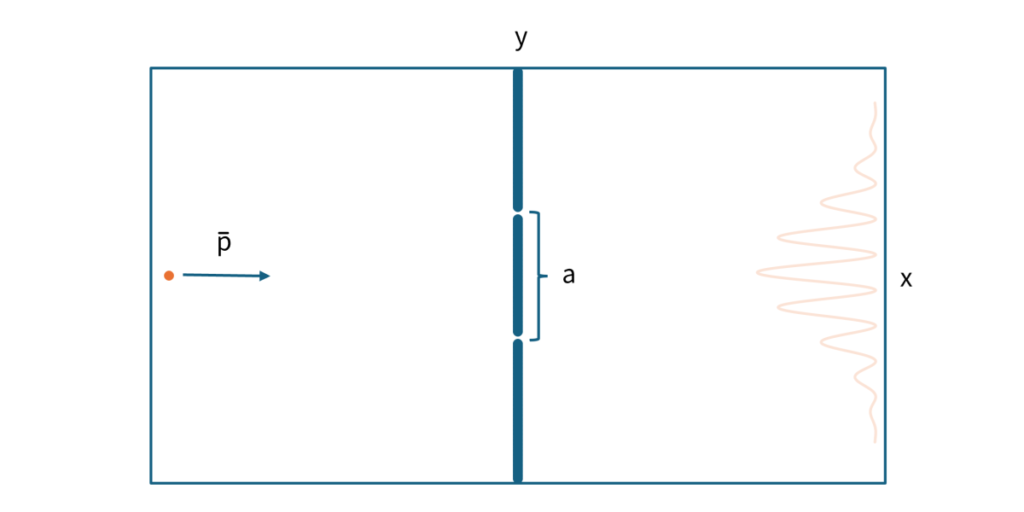
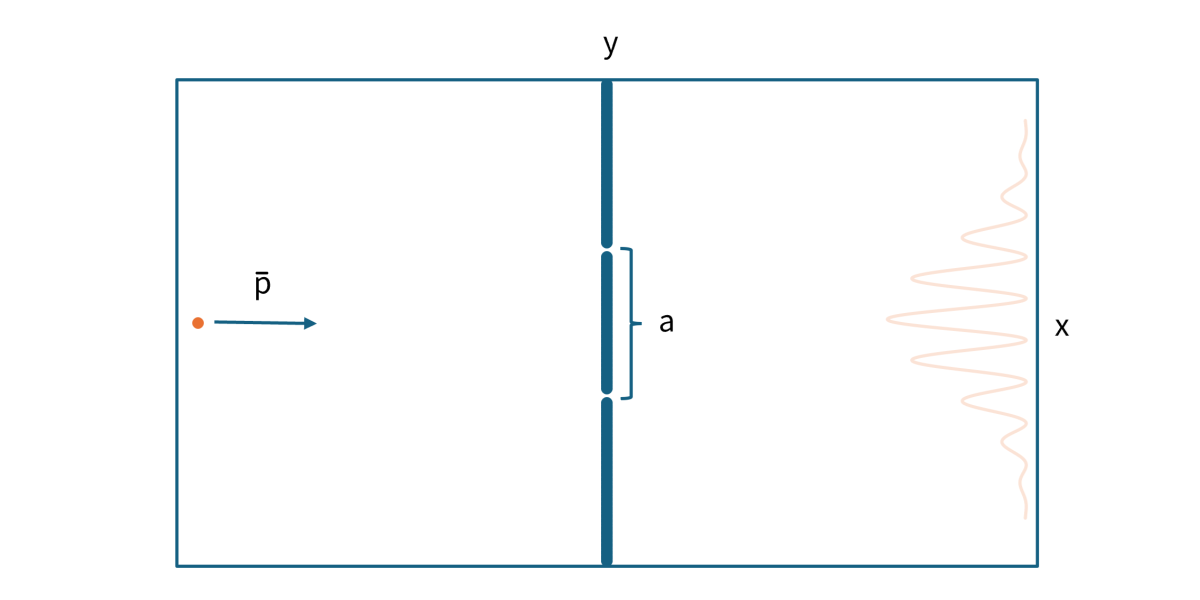
ここで、\(\small a\)はスリットの間隔、\(\small x,y\)はスリットの中心を原点とした座標の値、\(\small \bar{p}\)は\(\small x\)軸方向の運動量(の平均値)である。これを片方のスリットをふさいで同じ実験をすると波のような確率分布は消えて、正規分布に近いランダムな確率分布になってしまう、というのが二重スリット実験の概要である。1960年代ぐらいまでは思考実験であったが、実際の実験でも正しいことが確認されるようになったようである。特に有名なのは1980年代後半に行われた外村による実験だろう。
そのような結果を再現する方程式などあるわけないだろうと思うかもしれないが、近似的であるにしてもこの実験結果を再現する方程式が存在しており、それがシュレディンガー方程式ということである。ただし、シュレディンガー方程式で二重スリット実験の検出確率分布を計算する際は、一つの量子が上のスリットを通過した場合の波動関数と下のスリットを通過した場合の波動関数を合成して計算しなければならない。このことから推測されることとして、二重スリット実験において量子は一つの粒子であるかのように検出されるにもかかわらず、二つのスリットを同時に通過していると解釈しなければならないということである。この結果をシュレディンガー方程式を用いて導出しよう。
数学的な問題設定
二重スリット実験における量子の検出確率分布を求めるため、シュレディンガー方程式を用いた定式化を行う。スリットがあるため、この障壁をポテンシャル関数として定義するのかと思うかもしれない。しかし、スリット通過時点を境界条件(初期状態)とするため、障壁をポテンシャル関数として定義することはせず、自由状態におけるシュレディンガー方程式をそのまま適用する(自由状態におけるシュレディンガー方程式については
を参照。)。すなわち、基礎方程式は
\[ \small i \hbar\frac{\partial \psi(x,y,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \left(\frac{\partial^2 \psi(x,y,t)}{\partial x^2}+\frac{\partial^2 \psi(x,y,t)}{\partial y^2} \right) \]
である。境界条件(初期状態)はそれぞれ\(\small 1/2\)の確率で上のスリットと下のスリットを通過するものとして
\[ \small \begin{align*} &\psi(x,y,0) = \frac{1}{\sqrt{2}}\psi_{+}(x,y,0)+\frac{1}{\sqrt{2}}\psi_{-}(x,y,0) \\ &\psi_{\pm}(x,y,0) = \frac{1}{\sqrt{\pi}\sigma} \exp\left(-\frac{x^2+(y\pm\frac{1}{2}a)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}x \right) \ \end{align*} \]
と置く。自由状態同様に、どちらのスリットを通過するにしても座標には一定の不確定性があり、その不確定性の程度は\(\small \sigma\)で表す。上記の基礎方程式と境界条件をもとに解を求めれば、二重スリット実験における量子の検出確率分布を導出することができる。
二重スリット実験の確率分布を導出する前に、どちらのスリットを通過するかを明らかにした場合における確率分布を求める。片方のスリットをふさいで、どちらのスリットを通過したかを明らかにした場合、境界条件は
\[ \small \psi(x,y,0) = \psi_{\pm}(x,y,0) \]
のいずれかになる。しかし、この場合における基礎方程式と境界条件は自由状態におけるシュレディンガー方程式と同じものであるから
\[ \small y(t) \sim N\left(\pm \frac{1}{2}a, \frac{\sigma^2}{2} + \frac{\hbar^2}{2m^2\sigma^2}t^2 \right) \]
であり、干渉縞のようなものは生じず、正規分布に従うランダムな点として検出されることになる。したがって、二重スリット実験における干渉縞を生成させるためには、量子がどちらのスリットを通過したかを明らかにすることができないということになるだろう。言い換えれば、量子が二つのスリットを同時に通過しない限り干渉縞は生じない、ということを意味する。これは前節で説明した二重スリットの実験の説明と一致するものであることは理解できるだろう。
解の導出
例によって、基礎方程式と境界条件が
\[ \small \begin{align*} & i \hbar\frac{\partial \psi(x,y,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \left(\frac{\partial^2 \psi(x,y,t)}{\partial x^2}+\frac{\partial^2 \psi(x,y,t)}{\partial y^2} \right) \\ &\psi(x,y,0) = \frac{1}{\sqrt{2}}\psi_{+}(x,y,0)+\frac{1}{\sqrt{2}}\psi_{-}(x,y,0) \\ &\psi_{\pm}(x,y,0) = \frac{1}{\sqrt{\pi}\sigma} \exp\left(-\frac{x^2+(y\pm\frac{1}{2}a)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}x \right) \ \end{align*} \]
であるときの\(\small \psi(x,y,t)\)を求めよう。ただし、二重スリット実験では量子を検出するスクリーンは平らなものを使用するため、スクリーンの\(\small x\)軸の値を\(\small X\)と表して、\(\small \psi(X,y,t(X))\)と置いて解を求める。\(\small x\)軸方向の運動量の期待値\(\small \bar{p}\)が運動量の不確実性\(\small \hbar/\sqrt{2}\sigma\)を無視できるほど大きい値であると仮定して
\[ \small x(t) \approx \frac{\bar{p}}{m}t \; \Rightarrow \; t(X) \approx \frac{mX}{\bar{p}} \]
と近似する。問題自体は自由状態におけるシュレディンガー方程式と同じであるから、\(\small y\)軸方向の波動関数は
\[ \small \begin{align*} \psi_{\pm}(y,t)&= \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left(y\pm\frac{a}{2}\right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{\hbar}x – \frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left(y\pm\frac{a}{2}\right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right) \end{align*} \]
と計算できる。\(\small t\)を\(\small X\)で置き換えると
\[ \small \begin{align*} \psi_{\pm}(y,X)&= \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar X}{\bar{p}\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left(y\pm\frac{a}{2}\right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{2\hbar}X + \frac{\hbar X \left(y\pm\frac{a}{2}\right)^2}{2\bar{p}\sigma^4 \left(1 + \left( \frac{\hbar X}{\bar{p}\sigma^2} \right)^2 \right)} \right\} \right) \end{align*} \]
を得る。計算の簡略化のため
\[ \small \frac{\hbar X}{\bar{p}\sigma^2} \gg 1 \]
を仮定する。これは二重スリット実験では一般に正当化できる仮定であるということである(Xを非常に大きくとるということであり、実はスリットからスクリーンまでの距離は数十メートルから数百メートルとるらしい)。定数部分は計算が面倒なので後で規格化するとして、指数部分のみを計算すると
\[ \small \begin{align*} \psi_{\pm}(y,X)& \propto \exp \left(- \frac{\left(y\pm\frac{a}{2}\right)^2}{2 \sigma^2 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \times \exp \left(i\frac{\bar{p}}{2\hbar} \left\{X + \frac{\left(y\pm\frac{a}{2}\right)^2}{X} \right\} \right) \end{align*} \]
と近似できる。波動関数は
\[ \small \psi(y,X) = \frac{1}{\sqrt{2}}\psi_{+}(y,X) + \frac{1}{\sqrt{2}}\psi_{-}(y,X) \]
であったから、確率分布を計算すると
\[ \small \begin{align*} P(y,X) \propto & \;\exp \left(- \frac{\left(y+\frac{a}{2}\right)^2}{\sigma^2 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) + \exp \left(- \frac{\left(y-\frac{a}{2}\right)^2}{\sigma^2 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \\ &+2\exp \left(- \frac{a^2}{4 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right)\exp \left(- \frac{y^2}{\left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \cos\left( \frac{\bar{p}}{\hbar}\frac{ay}{X}\right) \end{align*} \]
となる。\(\small X\)を非常に大きくとるため、expの内部における\(\small a\)を無視できるものとして\(\small a \rightarrow 0\)とすれば
\[ \small P(y,X) \propto 2\exp \left(- \frac{y^2}{\left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \left(1+\cos\left( \frac{\bar{p}}{\hbar}\frac{ay}{X}\right) \right) \]
を得ることができる。これが二重スリット実験における干渉縞の確率分布であるということだった。ちなみに、最初の図で示した波打った確率分布はこの式から計算したものである。
二重スリット実験の解釈
二重スリット実験については、いくつかの解釈が存在する。列挙すると以下のようなものになるだろうか(それぞれの解釈について筆者は詳しくないので、間違いがあったらごめんなさい)。
- 確率解釈(統計的解釈、コペンハーゲン解釈)・・・波動関数は量子の観測確率分布を表しており、スクリーン到達時にその確率分布からランダムにサンプリングされて検出されているという解釈。量子の観測確率分布が波打つのは量子がそういう性質を持つ(シュレディンガー方程式に従う)ものとして(原理や公理として)受け入れることにする。
- 確率解釈(量子ポテンシャル)・・・量子はあくまで粒子であり、片方のスリットを通過してスリットに到達しているという解釈。デヴィッド・ボームやエドワード・ネルソンなどの学説に基づく。波動のような観測分布は量子がそのようなポテンシャル(パイロットウェーブ)をまとっているためとする。
- 粒子と波動の二重性(波束の収縮)解釈・・・量子は観測される前は波動として振舞い、観測されると粒子として振舞うという解釈。コペンハーゲン解釈に似ているが、どちらかと言えばコペンハーゲン解釈の批判者寄りの解釈に見える。観測することで実在を獲得するという考え方。アインシュタインの”観測していないときは月は存在していないとでもいうのか”とかシュレディンガーの猫に近い解釈だろう。
- 多世界解釈・・・観測することで世界が分岐しており、確率分布のうち観測されない別の世界も実は存在しているという解釈。決定論的な世界が無数に存在しており、どの世界が選択されるかが確率的に決定されているという世界観。Hugh Everett III世が提唱した。
- 主観解釈・・・量子の振る舞いが情報として人の意識に認識されることで波動関数が収縮するという解釈。アインシュタインの批判を肯定的に解釈したものだろうか?自己啓発系やスピリチュアル系の量子力学本の解釈と見ればよいと思われる。一応、発案者(Eugene P. Wigner、意外かもしれないが大御所の物理学者で1963年にノーベル物理学賞を受賞している)がいるらしいが、真偽は不明である。
- 観測が過去に干渉説・・・観測という行為が過去に影響を及ぼすために、どちらのスリットを通過したかが明らかにできないという説。二重スリット実験が時間が一方向にしか進まないと考えると現象の説明ができないことに起因するものと推測される。おそらく、ファインマン自身の説ではないだろうけど、ファインマンの経路積分(経路積分の計算は量子が過去に干渉していることを否定していない)から派生した解釈と思われる。
統計的解釈(コペンハーゲン解釈)と粒子と波動の二重性という解釈はしばしば同一視されるが、本稿では分けることにした。おそらく元のマックス・ボルンの解釈がこういうものであったのだろうと推測する。加えて、以下で説明する筆者の説明はある意味で常識外れの主張であるが、統計的解釈を拡張したものであり、一応正統派に属している考え方であると言いたいがために分けておいたという側面もある。変更点は量子の観測確率分布が波打つ理由を原理としては受け入れず、相対論的な時空の性質に求めるということである。筆者が考える二重スリット実験の解釈を仮説的であるが提示して終わりにしよう。
二重スリット実験は相対論的な現象
アインシュタインの特殊相対性理論から導かれるもっとも驚くべき結論のひとつは、時間という慣れ親しんだ概念は、根本的に間違っているということだ。・・・時間は絶対的に規則正しく、いつでもどこでも誰にとっても同じだと考えられていた。これに対してアインシュタインは「ノー」と言った。時間は伸びたり縮んだりし、人それぞれにとって流れ方が異なり、あなたの時間と私の時間は違う。
サイモン・シン、『宇宙創成』
前節で示した解釈が暗黙的に前提としている仮定として、空間や時間をユークリッド空間(古典力学的な空間)で考えているということが挙げられる。言い換えれば、空間を3次元ユークリッド空間\(\small R^3\)、時間を1次元\(\small R\)と仮定している。これはシュレディンガー方程式が古典力学からの類推から導出されていることに原因があると考えられる。しかし、実を言うと、二重スリット実験は光子についても成り立つし、電子の実験においても光速に近い速度で発射しないと現象をうまく再現できないと推測される。有名な外村の実験においても、電子を光速の40%近い速度で発射して実験を行っている。シュレディンガー方程式が導出する確率分布がその結果を近似的に再現しているというのがその実験結果であった。
このことから言える推測は、二重スリット実験を理解するためには相対論的な議論に基づかなければならないということである。光速の40%でも古典力学的な理論を破綻させるには十分な速さであるし、光子については当然相対性理論に基づいて考える必要がある。そして、前節で列挙した一般に提供される二重スリット実験の解釈はいずれもこの点を考慮していないという意味で、おそらく間違っているという推測を行うことができる。また、シュレディンガー方程式が導出する確率分布がその結果を再現していることから推測される仮説は、シュレディンガー方程式は実は(近似的であるにしても)相対論的な時空の上に定義された方程式であるということである。二重スリット実験の理解が困難である理由は、以下の2つの主張
- シュレディンガー方程式が二重スリット実験の結果を再現する
- シュレディンガー方程式は古典力学的な時空に対して定義された方程式である
が矛盾しているように見えるからである。筆者の仮説は2つ目の主張が実は間違っているために二重スリット実験の理解が困難になっているというものである。
筆者の著書や他の投稿で指摘しているように、相対論的な時空は
\[ \small x^2+y^2+z^2+c^2T^2=c^2t^2 \]
であり、時間を一次元\(\small t\)と仮定すると、空間は三次元球面\(\small S^3\)として扱わなければならない。
\[ \small S^3 = \{(x,y,z,s)|x^2+y^2+z^2+s^2=1\} \]
しかし、三次元球面がどのような図形であるかは我々は知ることができない。これは、地球の地図を作成する際に、二次元球面\(\small S^2\)を二次元のユークリッド空間上の平面\(\small I \in R^2\)に写像したいという場合に、伸縮なしに表現することができないということを考えれば、類推することができるだろう。
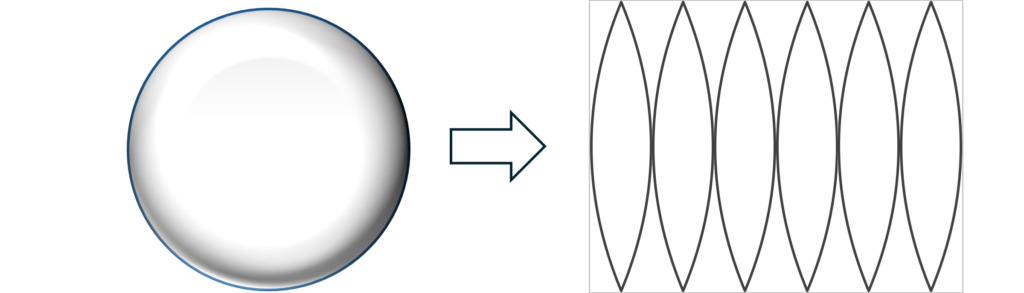
三次元球面を空間の伸縮なしに三次元ユークリッド空間上に表現することができないということであり、時間を一次元として扱うならば空間が伸びたり、縮んだりするものと考えなければならず、二重スリット実験をユークリッド空間上の現象と捉えていることがそもそも間違っているということになるだろう。
反対に、空間をあくまで三次元ユークリッド空間\(\small R^3\)と仮定する場合、複素関数で表現された二次元の時間というものを考えなければならない。すなわち、
\[ \small \begin{align*} &x^2+y^2+z^2+c^2T^2=c^2\zeta_{xyzt}\zeta_{xyzt}^\ast \\ &\zeta_{xyzt} = \frac{1}{c}\sqrt{x^2+y^2+z^2}+iT = te^{i\theta_{xyzt}} \end{align*} \]
であり、座標ごとに異なるものとして定義される時間\(\small \zeta_{xyzt}\)が本来の時間の性質を表すものであることになる。この場合、運動する量子に適用される時間が伸びたり、縮んだりする結果として二重スリット実験のような現象が現れるという解釈になるだろう。
また、量子が2つのスリットを同時に通過しているということは不可思議に感じるかもしれないが、量子の本質は確率分布(ノイズ)であり、本来空間的な広がりを持っているものと推測される。検出される際に、その確率分布の中から一点がサンプリングされる形で検出されるために、二重スリット実験のような結果が生じると考えることができる。言い換えれば、粒子や波動という概念は人間が観測できる現象を説明するために便宜的に創り出した”モデル”(仮想的な概念)であり、現実に実在するとは言えない概念であるということである。多くのオカルト的な解釈が生み出される原因の一つとして、このモデルに過ぎない粒子や波動という概念を実在的なものと勘違いしていることが挙げられるだろう。
以上が筆者が考える二重スリット実験の解釈である。もし筆者の考え方が正しいと仮定すると、二重スリット実験を理論的に理解するには、相対論的な量子力学(場の量子論)や量子電磁気学の理論が必要になる。そもそも学部生レベルの量子力学の知識では不足しており、大学院の博士課程ぐらいの量子力学の知識がないと理解することは不可能であるということになる(それでも不可能かもしれないけど)。学部生レベルの量子力学の知識をこねくり回して正しい結論が得られるなどという甘い期待を持って挑戦しない方がよいかもしれない、ということは指摘しておいてもよいだろう。
参考文献
[1] 朝永振一郎 (1997), 量子力学Ⅰ(第2版), みすず書房
[2] 朝永振一郎 (1997), 量子力学Ⅱ(第2版), みすず書房
[3] 平野要 (2022), 多時間理論による量子力学ー二重スリット実験に関する一考察ー, Amazon Kindle Store(英語訳:Hirano, Kaname (2022), Quantum Mechanics with Multi-Time Theory, Amazon Kindle Store.)
[4] 平野要 (2024), 複素関数とシュレディンガー方程式, Amazon Kindle Store(英語訳:Hirano, Kaname (2024), Complex Functions and Schrödinger Equation, Amazon Kindle Store.)
[5] Tonomura, Akira et al (1989), Demonstration of Single‐electron Buildup of an Interference Pattern. American Journal of Physics, 57, 117-120.
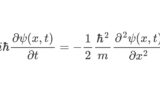


コメント