※ChatGPT画伯作, “A visually striking representation of the Prisoner’s Dilemma.”
勝利確率を正確に計算するプレイヤーに勝つことができるか?
手札と共通カードから自分が勝利する確率を正確に計測し、一貫性を持ったリスク管理をするプレイヤーがいるとする。これは前回の投稿で示したモンテカルロシミュレーションで確率を計算し、それに応じて最適なベット金額を決定するNPCが該当する。筆者は現状このレベルのプレイヤーには勝てないのであるが、これに勝つ方法はあるだろうか?実をいうとこれには攻略法が考えられている。
推定した勝利確率\(\small p\)に対して、最適なベット金額\(\small f\)を計算するのであるから、最適なベット金額は\(\small f=\pi(p)\)と推定した勝利確率の関数として表すことができる。他のプレイヤーから見た場合、手札から推定される確率\(\small p\)は非公開情報であるためわからないのであるが、実をいうとベット金額\(\small f\)はある程度の精度で共通の情報として公開されている。典型的には、レイズやベットをしたときにどの程度の金額を指定したか、あるいは、どの程度の金額までコールするかということで表明される。言い換えれば、推定した勝利確率\(\small p\)は非公開情報であるが、最適なベット金額\(\small f\)は他のプレイヤーが知ることができる公開情報であるということになる。この場合、もし\(\small f=\pi(p)\)の関数型が知られてしまっている場合、そのプレイヤーが持っている手札の強さを
\[ \small p^\ast = \pi^{-1}(f) \]
と推測することができることになる。
このように、相手プレイヤーの行動パターンを知ることができた場合に、その行動パターンを利用して勝率を上げたり、期待リターンを上げる戦略を搾取戦略(エクスプロイト戦略)という。勝利確率を正確に計算し、それに基づいて決まった賭け金比率\(\small f\)で賭けるという戦略は、搾取戦略を用いられない限りにおいては最強の戦略であるかもしれないが、手札を相手プレイヤーに読み取られる可能性が高い戦略という意味で、それほど強い戦略ではないのかもしれない。
不完全情報ゲームでは、公開されている情報から隠されている情報を推測するというオペレーションが非常に重要であり、現実社会においてもこういった戦略を用いることで他者との競争で優位性を得ることができることは理解できるだろう。例えば、隠されている敵の情報や意思決定の結果を盗み取ることを政治や軍事では諜報(インテリジェンス)という。典型的には、相手の組織にスパイを送り込んだり、組織に不満を持つ裏切り者から情報を聞き出す行為を指すが、エクスプロイト戦略のように一般に公開されている情報から逆算して敵の隠れた情報や意図を推理するという手法(OSINT: Open Source Intelligence)もよく用いられているらしい。
ベットから手札を推測する方法
勝利確率を正確に計算し、Kelly基準やCRRA型効用関数でベットの意思決定を行うNPCは、勝利確率\(\small p\)に対して、以下の賭け金比率\(\small f\)に近くなるようにベットしてくる(プレイヤーが4人の場合)。
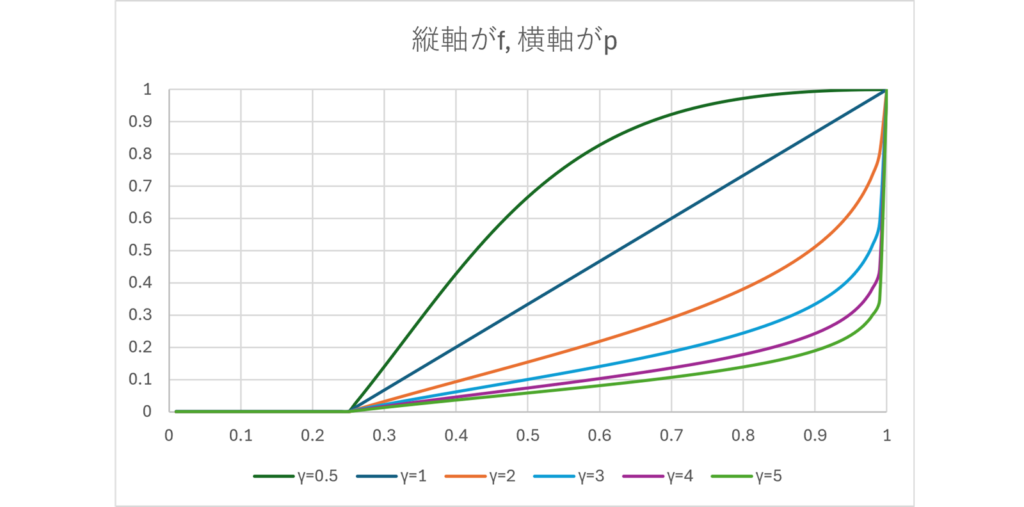
NPCのリスク回避度が分かっていれば、推定している勝利確率\(\small p\)がどの程度の水準であるかが分かることになる。相手の推定勝利確率が自分の勝利確率より大きい場合、たとえ強い手札であってもベットを吊り上げることは避けるべきであるし、反対に自分の手札がイマイチであっても、相手の推定勝利確率がそれより低そうであれば強気に攻めるということもできることになる。
また、推定している勝利確率\(\small p\)が分かった場合、手札の組み合わせによっては相手が持っている手札を特定できる場合もある。例として、4人プレイのテキサスホールデムで、フロップにおける公開カードが以下のようなものであったとする。
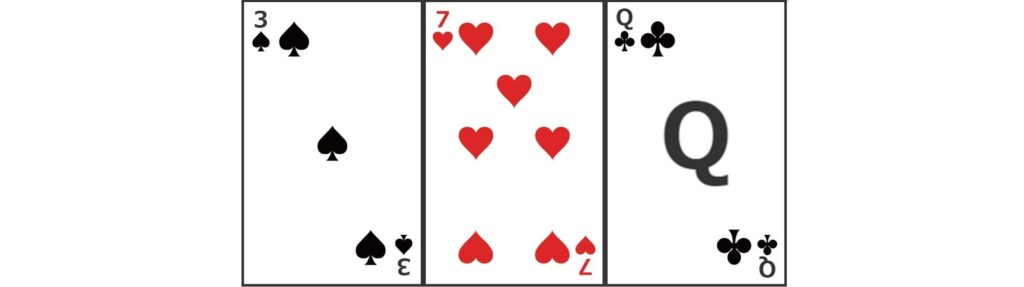
このとき、対戦プレイヤーがレイズした結果、対戦相手が勝利確率を50%程度である(期待リターンでは\(\small 4\times0.5-1=100\%\))と見積もっていることが推定できたとする。この公開カードでは、ストレートやフラッシュが成立する可能性はないため、役ができているとしたら、ワンペア、ツーペア、スリーカードのいずれかだろう。しかし、この公開カードでは3と7のツーペアでも65%近い勝利確率であるため、できている役はワンペアであると推定できる。加えて、各ランクのワンペアの勝率は3のワンペアが25%、7のワンペアが33%、Qのワンペアが53%程度である。したがって、レイズしたプレイヤーの手札の1枚はQであると推定することができる。また、もう一枚は3,7,Q以外のいずれかのカードであるというところまで範囲を絞り込むことができる。
このように、相手の行動から相手が持っている可能性がある手札を絞り込んだ組み合わせの範囲はレンジ(そのままだけど)と言われる。もしこのレンジより、自分の手札が強いと考えればベットを吊り上げて勝負すればよいし、弱いと判断すればFoldするという判断ができるだろう。このような方法で対戦プレイヤーの手札を推測することで、自分が勝利する確率を正確に計測し、一貫性を持ったリスク管理をするプレイヤー(NPC)に勝利することも不可能ではないということになる。
カウンター・エクスプロイト
コンピュータのアルゴリズムであれば、自分の手札が読まれているなどと気づくことはないだろうが、現実の人間であれば、一定の経験を積めばもしかしたら相手は自分の行動から自分の隠している手札を推測しているかもしれないと気づくだろう。また、自分自身も対戦相手の行動から相手の思惑を読み取ろうとしているかもしれない。このことに気づいた場合、何の対策も打つことなく搾取され続けるという人はあまり多くはないだろう。相手に自分の手の内を読み取られないように偽りの行動をすることで騙そうとしたり、ランダムな要素を取り入れることで予測を行いづらくするといった対策をとることになる。
例として、政治や軍事におけるインテリジェンスを考えると、敵対国が自国の情報や意思決定について諜報活動を通じて盗み出していることが分かっているとする。この場合、そういった情報にアクセスできる幹部にわざと偽の情報を教えたり、個別の幹部ごとに異なる情報を伝えることで、敵対国に情報を誤認させたり、スパイや裏切り者を特定しようという戦略が採られることがある。また、相手が公開情報から自分たちの内部情報を推測する強力な手段を備えていると考える場合に、やはり誤認を誘発するためにわざと誤った公開情報を提示するという操作が行われることもある。このような活動はカウンター・インテリジェンスといわれる。
同様にして、テキサスホールデムにおいても、自分のベット戦略\(\small f=\pi(p)\)が対戦プレイヤーに推測されていると考える場合、対戦プレイヤーに誤った意思決定をさせる目的や、自分のベット戦略の推測を妨げる目的で自分の手札の強さとは異なるベットを提示することがある。こういった戦略はカウンター・エクスプロイトといわれる。典型的には、手札より強気にベットするブラフや手札より弱気に見せて他のプレイヤーに賭け金を積み上げさせようとするスロープレイという手法がそれに該当する。ブラフやスロープレイを用いない場合であっても、自分のベット戦略の推測を妨げる目的でベット戦略にランダムな要素を組み込み、同じ手札の強さについて異なるベットを提示するといった戦略が採られることもある。
カウンター・エクスプロイトをベット戦略に組み込む場合、推定勝利確率\(\small p\)が同じ値でも、確率的に異なる行動を採用することになる。この場合、ベット戦略\(\small f = \pi(p)\)における\(\small f\)はスカラー値ではなく、採用すべき賭け金額の確率分布を返す関数ということになる。このように確率分布に従って、複数の行動を確率的に選択する戦略をゲーム理論の用語で混合戦略(Mixed Strategy)という。反対に、同じ状態に対して常に同じ行動を行う戦略は純粋戦略(Pure Strategy)と言われる。テキサスホールデムなどの不完全情報ゲームでは、純粋戦略が最適解であることは稀であり、混合戦略の解を考える必要があるだろう。
テキサスホールデムとナッシュ均衡
怪物と戦うものは誰であろうと、その過程で怪物にならないよう心がけなければならない。 あなたが深淵をのぞき見ようとしているとき、深淵もまたあなたをのぞき見ようとしているのだ。
フリードリヒ・ニーチェ、『善悪の彼岸』
対戦相手のベット戦略から、相手の手札を予想することができるし、混合戦略を取り入れることで対戦相手が自分の手札を予測することを妨げることができるということを説明した。これで完璧な戦略だと思うかもしれない。しかし、現実には対戦相手も同じようにして、混合戦略を用いてあなたが手札を予測することを妨げてくるかもしれないし、ベット戦略自体も自分の手札だけから定めているわけではないかもしれない。エクスプロイト戦略やカウンター・エクスプロイトの行き着く先はいたちごっこだろう。あなたが対戦相手の戦略に対して対策を立てれば、対戦相手もその対策に対して別の対抗策を考えてくる。その対抗策で負けるようであれば、あなたは別の対抗策を考えることになる。この繰り返しが行き着く先はどのようなものであろうか?
自分自身の手札の勝利確率と相手のベットから推測される相手の手札の強さを考慮したベット戦略を考える。この場合、最適な賭け金比率\(\small f\)は自身の手札の勝利確率\(\small p_1\)と相手のベット\(\small f_2\)から推測される勝利確率\(\small p_2 = \pi_2^{-1}(f_2)\)の関数であるから、
\[ \small f_1 = \pi_1(p_1, p_2) = \pi_1(p_1, \pi_2^{-1}(f_2)) = \pi_1(p_1, f_2) \]
と表すことができる。しかし、もし対戦相手も自分の手札を推測したうえでベット戦略を考えている場合
\[ \small f_2 = \pi_2(p_1, p_2) = \pi_2(p_2, \pi_1^{-1}(f_1)) = \pi_2(p_2, f_1) \]
と表現されなければならない。言い換えれば、\(\small f_2\)は\(\small f_1\)の関数でもあるため、これを\(\small f_1\)の式に代入すると
\[ \small f_1 = \pi_1(p_1, f_2) = \pi_1(p_1, \pi_2(p_2, f_1)) = \pi_1(f_1 \: | \:p_1,p_2) \]
と表されることになる。同様にして、
\[ \small f_2 = \pi_2(f_2 \: | \:p_1,p_2) \]
と表現できる。
最適な戦略では、引数に代入される\(\small f\)と関数の返り値の\(\small f\)は同じ値でなければ、相手の戦略を間違って推測することになるため、矛盾することになる。したがって、最適解では
\[ \small \begin{align*} &f_1^\ast =\pi_1(f_1^\ast \: | \:p_1,p_2) = \pi_1(p_1, f_2^\ast) \\ &f_2^\ast =\pi_2(f_2^\ast \: | \:p_1,p_2) = \pi_2(p_2, f_1^\ast) \end{align*} \]
が成り立たなければならない。このように、引数と関数の返り値が一致する点をその関数の不動点(Fixed Point)という。関数を何回作用しても値が変わらないということであり、
\[ \small f_1^\ast = \pi_1 \circ \pi_1 \circ \cdots \circ \pi_1 (f_1^\ast) \]
となる点である。二人のプレイヤーのベット戦略を集合で表し、その集合を引数と受け取り、ベット戦略を集合として返す関数を考えれば、
\[ \small \{f_1^{\ast}, f_2^{\ast} \} = \pi\left(\{f_1^{\ast}, f_2^{\ast} \}\: \Big| \: p_1,p_2 \right) \]
と表すことができる。このよう関数\(\small \pi\)は集合値関数(Set-Value Function)と言われる。二人のプレイヤーの最適なベット戦略はこの集合値関数の不動点として表現されることになる。
プレイヤーが採用できる集合の組み合わせが有限であり、かつ、戦略関数\(\small \pi\)が連続関数である場合、この不動点が存在することは角谷の不動点定理といわれる位相幾何学の定理から証明される。ゲーム理論では、この不動点として表現される戦略のことをナッシュ均衡戦略という。ゼロサムゲームにおけるナッシュ均衡戦略は、誰かが自発的に損をしない限りこれ以上自分の利得(効用)を改善することができない(パレート最適な)戦略であることが知らており、テキサスホールデムのように他者と協力することが基本的にないゲームでは、最終的な到達点となる戦略であると考えられる。テキサスホールデムにおける最適な戦略はこのナッシュ均衡戦略であり、ナッシュ均衡戦略を意識してプレイする方法はGTO(Game Theory Optimal)戦略と言われているようである。
テキサスホールデムでは各プレイヤーは対称であるから、自分自身と同じようにナッシュ均衡戦略を採用するプレイヤーを前提として自身のナッシュ均衡戦略を計算することで最適な戦略を求めることができる。現実には、テキサスホールデムのカードやベットの組み合わせは天文学的な数のパターンが存在するため、ナッシュ均衡戦略がどのようなものであるかを厳密に計算することは不可能であると思われる。ただし、プリフロップでは考えうるパターンの数が限定されるため、ナッシュ均衡戦略に従った各手札で採用するべき混合戦略が計算されているらしい。結果として、プロ同士のプレイでは8割から9割がプリフロップで決着がついてしまうようである。役が揃うかどうかワクワクしながら、カードを開こうとしているうちは素人ということなのかもしれない。
また、ナッシュ均衡戦略はすべての対戦相手に対して最適な戦略ではないことに注意する。どのような対戦相手に対しても優位性を奪われることがない(エクスプロイトされることがない)戦略ではあるが、対戦相手のベット戦略が読める(ナッシュ均衡戦略から外れた戦略を採用している)場合は、それに合わせて戦略を変えた方が期待リターンが上がることがある。ただし、これを実行するためには、対戦相手のベット戦略についてある程度データを収集したり、前提を置いて計算する必要がある。知り合い同士でプレイする場合やプレイスタイルに特徴がある有名プレイヤーが集まるトーナメント大会などを除けば、一般的なシチュエーションでこの条件が満たされることはほとんどないだろう。
また、ナッシュ均衡に基づいた混合戦略は人間にとってはかなり苦痛を感じる意思決定方法である可能性がある。例えば、手札がAQo(柄が異なるAとQ)であった場合に、プリフロップでは多くの場合レイズするかコールするかだろうが、混合戦略では手札を読み取られることを防止する目的で一定の確率でFoldしなければならないということになるかもしれない。反対に、弱い手札であっても一定の確率で強気のレイズ(ブラフ)をしなければならないということになる。結果として一定のチップを失うことになる可能性が高いが、このとき、あなたは一定の確率でFoldする(レイズする)という選択を選ぶことができるだろうか?よほど強い意志を持って実行しない限り、強い手札の時に強いベットをして、弱い手札の時にFoldするという単調な戦略に陥ってしまう可能性があるということは指摘できるだろう。
加えて、テキサスホールデムの勝敗は運の良し悪しに左右される要素が多分に含まれている。勝率や期待値を正確に計算して戦略を実行した結果、目に見えて強くなったことが実感できるようになるには相当の回数のプレイをこなさなければならないかもしれない。10回や20回のプレイでは確率や期待値は収束しないということである。これが何回であるか不明であるが、確率や期待値が収束すれば優れた戦略であると信じて苦痛を感じる意思決定方法を繰り返すためには、相当の精神力を要求されることになるかもしれない。
手札の推測をどうやってゲームに反映するか
文章が長くなったので、これはまた別の投稿で考察するが、テキサスホールデムにおいて期待効用に基づいてベット戦略を決めるという方法は入門者からせいぜい中級者レベルのプレイヤーが行う意思決定方法であり、上級者以上は全く異なる方法で意思決定を行っている可能性が高いということが分かるだろう。期待効用を最大化するプレイヤーより強いプレイヤーや戦略の幅を持ったNPCを考えるためには、これを考慮した意思決定アルゴリズムを考える必要があるのだろう。
参考文献
[1] Acevedo, Michael, Modern Poker Theory: Building an Unbeatable Strategy Based on GTO Principles, D&B Publishing, 2019. (日本語訳: 現代ポーカー理論: GTOの理論と実践, 星雲社).


コメント