※ChatGPT画伯作 “A dynamic and detailed illustration of a Texas Hold’em poker game in progress.”
テキサスホールデムとKelly基準
前回の投稿で、ひとまずテキサスホールデムのルールの枠組みは開発できたと思われる。ただし、対戦プレイヤーがランダムにベットを打ってくるだけであり、人間らしくないだろうし相当に弱いプレイヤーであると推測できる。そのため、人間が行うように手札と共通カードから自分が勝てる確率がどの程度であるかを推測し、それに基づいて最適な意思決定を行う対戦プレイヤーを考えよう。
最初に、手札と共通カードから勝率を推測する方法であるが、これはモンテカルロシミュレーションで求めればよいだろう。10000回も行えばほぼ正しい解に収束するため、これに基づいて賭ける金額を決定するアルゴリズムを定めれば良い。これは過去の投稿で考察したようにKelly基準やCRRA型効用関数を使えばよいだろう。いくつかの理由があるらしく、テキサスホールデムにおける人工知能ではリスク中立に近い効用関数を用いるらしいが、人間の自然な判断では相応の程度でリスク回避的になると予測できる。そのため、本稿ではリスク回避的な効用関数における意思決定を考えよう。
使用する記号を以下のように定義する。
- \(\small p\):推定した勝利確率
- \(\small \alpha\):勝利した時に得られる利益(オッズ)
- \(\small \beta\):すでにFoldしたプレイヤーが投入したチップの合計
- \(\small n\):現在時点でFoldしていないプレイヤーの数
- \(\small W\):プレイ開始前に保有していた自分(意思決定主体)のチップ
- \(\small b\):すでにポットに投入した自分のチップ
- \(\small c\):現在のレート(コールする際に投入する必要があるチップの数)
- \(\small m\):ミニマムレイズ(ミニマムベット)の金額
最初に、Kelly基準(対数型効用関数)従ってベットする金額を定める方法を考える。テキサスホールデムではオッズは、すでにフォールドしたプレイヤーが投入したチップ\(\small \beta\)に残っているプレイヤー人数\(\small n\)は自分と同じ金額を賭けるものと仮定して
\[ \small \alpha = n(fW)+\beta \]
と計算すればよいだろう。この時の最適な賭け金比率\(\small f\)(チップの量は\(\small fW\))を求めよう。
自分が既にポットに\(\small b\)だけチップを投入してる場合、Foldした時の効用関数は
\[ \small E[U_{\text{Fold}}] = U_{\text{Fold}} = \ln\left(1-\frac{b}{W}\right) \]
で計算できる。現在のベット金額が\(\small c\leq W\)である場合、Call(Check)する場合は、その分だけチップを投入しなければならないので、期待効用は
\[ \small E[U_{\text{Call}}] = p\ln\left(1+\frac{\alpha-c}{W}\right)+(1-p)\ln\left(1-\frac{c}{W}\right) \]
と計算できる。最後にレイズする場合は、現在のベット金額にミニマムレイズ\(\small m\)を足した金額以上に設定する必要がある。ただし、この中から最適なレイズ金額を選択することができるため、
\[ \small \begin{align*} E[U_{\text{Raise}}(f)] &= \max_{fW \geq c+m} p\ln\left(1-f+\frac{\alpha}{W}\right)+(1-p)\ln(1-f) \\ &= \max_{fW \geq c+m} p\ln\left(1-f+nf+\frac{\beta}{W}\right)+(1-p)\ln(1-f) \end{align*} \]
の解が最適なレイズ額になる。これは解析的に解くことができて
\[ \small \frac{\partial }{\partial f}E[U_{\text{Raise}}(f)] = p\frac{n-1}{1-f+nf+\beta/W}-(1-p)\frac{1}{1-f}=0 \]
を満たす\(\small f\)を計算すればよい。整理すると
\[ \small f^{\ast} = \max\left\{\frac{np-1}{n-1}-\frac{1-p}{n-1}\frac{\beta}{W}, 0 \right\} \]
が解である。最終的な意思決定は、Fold,Call,Raiseでそれぞれ期待効用を計算し、最も値が高い選択肢をNPCの行動として決定すればよい。レイズする場合は最適な\(\small f^\ast\)に近い切りがより数値を選択すればよいだろう。\(\small f^\ast W<c+m\)の場合はミニマムレイズの金額における効用関数と比較する必要があることに注意する。
懸念点として、テキサスホールデムでは意思決定のタイミングが4回あり、かつ、一度引き上げてしまった賭け金は引き下げることができない。そのため、厳密には動学的最適化問題として解かなければならない。そのため、各意思決定の回で静的な効用関数を最大化すると元の効用関数よりアグレッシブな行動に見えるかもしれない。しかし、ゲームではとりあえず各意思決定の回でその都度最適な選択をするにとどめておく。また、Kelly基準ではAll-inを許容しないが、多くのチップをポットに入れてしまっている状況でオールインになる場合に必ずFoldするというのは不自然に見える。そのため、効用を計算する際の\(\small W\)は実際のチップ保有量に一定の値を足した(1%~5%ぐらい下駄をはかせた)値にした方が良いかもしれない。
CRRA型効用関数の場合
Kelly基準の計算はCRRA型効用関数に容易に拡張できるので計算しておこう。ゲームに登場するNPCとしては、リスク回避的なプレイヤーや強気でベットしてくるプレイヤーなどバリエーションがあった方が良いため、リスク回避度に応じた意思決定ができるようにしておくとよいだろう。
CRRA型効用関数は
\[ \small u(w) = \left\{ \begin{array}{ll}\frac{w^{1-\gamma}-1}{1-\gamma},& \quad \gamma \neq 1 \\ \log(w), & \quad \gamma=1 \end{array}\right. \]
であったから、Foldする場合とCallする場合の期待効用はそれぞれ
\[ \small \begin{align*} &E[U_{\text{Fold}}] = \frac{(1-b/W)^{1-\gamma}-1}{1-\gamma} \\ &E[U_{\text{Call}}] = p\frac{(1+(\alpha-c)/W)^{1-\gamma}-1}{1-\gamma}+(1-p) \frac{(1-c/W)^{1-\gamma}-1}{1-\gamma} \end{align*} \]
と計算できる。レイズする場合の最適化問題は
\[ \small E[U_{\text{Raise}}(f)] = \max_{fW \geq c+m} p\frac{(1-f+nf+\beta/W)^{1-\gamma}-1}{1-\gamma}+(1-p)\frac{(1-f)^{1-\gamma}-1}{1-\gamma} \]
と表すことができる。\(\small f\)について微分すると
\[ \small \frac{\partial }{\partial f}E[U_{\text{Raise}}(f)] = p\frac{n-1}{(1-f+nf+\beta/W)^\gamma}-(1-p)\frac{1}{(1-f)^\gamma}=0 \]
であるから、この式を満たす\(\small f\)を計算すればよい。整理すると
\[ \small \begin{align*} &f^{\ast} = \max\left\{\frac{\psi}{\psi+n}-\frac{1}{\psi+n}\frac{\beta}{W}, 0\right\} \\ &\psi = \left(\frac{p(n-1)}{1-p}\right)^{\frac{1}{\gamma}}-1 \end{align*} \]
が解である。最終的な意思決定は、Fold,Call,Raiseでそれぞれ期待効用を計算し、最も値が高い選択肢をNPCの行動として決定すればよい。以上により、リスク回避度\(\small \gamma\)に応じたプレイヤーの意思決定を定めることができる。
プレイヤーのプレイスタイル
単純に勝利確率を推定し、一定のリスク回避度に基づいてベット戦略を決定する以外にも、プレイヤーの行動を決める要素が存在する。推定した勝利確率をそのまま用いずに、客観的な勝利確率より強気に推定するプレイヤーや、反対に弱気に推定して手札が強い時以外は参加しないというプレイスタイルをとるプレイヤーが存在することが知られている。テキサスホールデムのプレイスタイルのタイプとして、一般的に以下の4種類のタイプがあると言われる。
- ルース(Loose)・・・全般的にFoldする確率が低く、参加率が高いプレイヤー
- タイト(Tight)・・・手札が弱いとFoldする確率が高く、強い手札以外は参加しないプレイヤー
- アグレッシブ・・・レイズを積極的に行い、1プレイ当たりの賭け金率が高いプレイヤー
- パッシブ・・・1プレイ当たりの賭け金率が低く、高くなるとFoldするプレイヤー
本稿の概念を用いれば、これらは以下のように定義することができるだろう。
- ルース・・・勝利確率の推定において、上方にバイアスがかかっているプレイヤー
- タイト・・・勝利確率の推定において、下方にバイアスがかかっているプレイヤー
- アグレッシブ・・・リスク回避度\(\small \gamma\)が低いプレイヤー
- パッシブ・・・リスク回避度\(\small \gamma\)が高いプレイヤー
ルース/タイト、アグレッシブ/パッシブは組み合わせが可能であり、タイトでアグレッシブなプレイヤーやルースでパッシブなプレイヤーなど、リスク回避度だけで見ると矛盾するようなプレイスタイルも表現することが可能である。
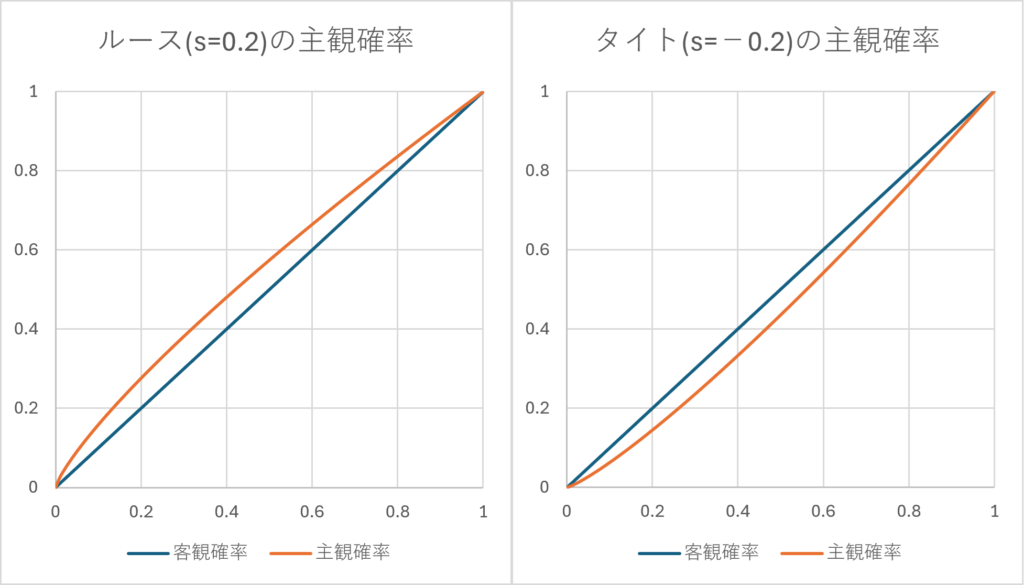
主観的な勝利確率の推定を
\[ \small p^{\ast} = p^{(1-s)} \]
と行う場合、\(\small s < 1\)がスタイルパラメータであり、\(\small s>0\)であればルースなプレイヤー、\(\small s<0\)であればタイトなプレイヤーということになる。
また、ルースかタイトは序盤(フロップ、プリフロップ)と後半(ターン、リバー)で異なる可能性もあるだろう。これはプリフロップにおけるスタイルパラメータを\(\small s_p\)、リバーにおけるスタイルパラメータを\(\small s_r\)とおいて
- プリフロップ:\(\small s = s_p\)
- フロップ:\(\small s = 2/3\times s_p+1/3\times s_r\)
- ターン:\(\small s = 1/3\times s_p+2/3\times s_r\)
- リバー:\(\small s = s_r\)
のように調整しても良いかもしれない。例えば、\(\small s_p>0\)だが\(\small s_r=0\)である場合、序盤はルースなプレイヤーであるが、後半になると客観的に確率を評価するプレイヤーということになるだろう。
計算した確率に一定のバイアス(掛け目)を掛けるように調整するなどして、プレイヤーとしての性格を表現する方法はNPCの弱体化につながると思うかもしれない。誤った確率に基づいてベット戦略を考えるということであり、大きな掛け目を掛ければもちろん弱体化する。しかし、ある程度の水準ではプレイヤーの性格(プレイスタイル)を表すものであり、必ずしもプレイヤーの弱体化にはつながらないと推測される。この理由は次節の内容から理解できるだろう。
NPCの強さの設計(失敗例)
ゲームを作るためにはユーザが倒すことができる強さ(弱さ)に設計する必要がある。強すぎて勝てないNPCが相手ではやる気がなくなってしまうだろう。そのため、実際に実装するNPCの意思決定ロジックはある程度弱いものや欠点があるものにしなければならない。まあ、ゲームなどというものをやる一番の理由はゲームをクリアして自己肯定感を得たいからだろう。上記の仕様(Kelly基準)でNPCのロジックを実装してみて、自分で対戦してみたのであるが、正直に言って今の筆者(ルールを覚えたのがつい最近ぐらいだけど)が太刀打ちできるレベルではないぐらい強くなってしまった。油断するとすぐにベットが吊り上げられる上に、そのときに限って相手の手札が強いと感じた。強い手札が来た時に多くのチップを一気に奪いたいのであるが、手札が弱いとあっという間にFoldしてしまい、ほとんどチップを得ることができない。というわけで、プログラムの分際で不愉快だから弱体化してやろうというのが本節の趣旨である。
そこで賢い僕は考えました。確率を正確に推測できているから強いのだろう、これを妨害してやれば弱体化できるだろう、と。これを行うには確率推定の誤差をモデリングすればよく、推定した正しい確率\(\small \bar{p}\)に正規分布のノイズを加えてモデリングすることで容易に実現できるだろう。すなわち、
\[ \small p = \bar{p}+\epsilon, \quad \epsilon\sim N(0,\sigma^2) \]
と推定し、\(\small 0 \leq p \leq 1\)を満たすように値を丸めればよい。プレイヤースキルの低い対戦プレイヤー程、推定誤差\(\small \sigma\)が大きくなるように設定することで、プレイヤーの強弱を表現することができるだろう。
実装して試した結果であるが・・・相手の手や行動が読めないという意味で、むしろ凶悪化してる気がする・・・。実際に、確率推定の誤差があるKelly基準と推定誤差がないKelly基準のNPC同士を戦わせてみたところほぼ互角であったし、人間が見ると確率推定の誤差があるKelly基準の方が手札とベットの関係性が分かりづらくなっている分だけ、行動が読めなくなってしまっているという意味で凶悪になっている。このように考えると、正確な勝利確率の推定ができるということはある程度までは強さに貢献するが、一定の程度を超えるとほとんど貢献しなくなるということが言えるかもしれない。
前節において、計算した確率に一定のバイアスを掛けることでプレイヤーのプレイスタイルを表現することが必ずしも弱体化にはつながらないということを述べた。上記のように強い手札を強いものとし、弱い手札を弱いものとしてある程度判定できていれば、そこから確率が多少ずれてもプレイヤー自身の強さには大きな影響を及ぼさないというのがその理由である。テキサスホールデムのプレイヤーが強くなりたいと考える場合に、真っ先に重要視することは様々局面における正しい勝利確率を覚えることだろうし、最初のうちはそれで強くなれているような気分になることもできるだろう。しかし、ある程度までいくとそれを突き詰めてもプレイヤースキルの向上につながらず、壁に直面してしまうということが起こるのではないだろうか?一通り正しい勝利確率を推定する能力を身に着けたにも関わらず、相変わらずプレイヤーとして弱いと感じるようであれば、次のような問題を抱えている可能性を考慮する必要がある。
初心者プレイヤーの弱さの源泉
天国へ行く最も有効な方法は、地獄へ行く道を熟知することである。
ニッコロ・マキャベリ
前節の内容から正しい勝利確率が推定できないことに弱さの源泉があるという考え方は一定の程度までは正しい仮説であるとしても、現実には間違っていることが分かった。それであるにもかかわらず、このゲームにおいて強いプレイヤーと弱いプレイヤーの間には明確な差異があるように見えるし、それがあるからこそ競技としてプレイされているゲームなのだろう。それでは、強いと感じるプレイヤーと弱いと感じるプレイヤーの違いはどこにあるのだろうか?一つの仮説は、正しく勝利確率を推定していたとしても、弱いプレイヤーはその確率に応じた適切な行動をとっていないことに原因があるというものである。
例えば、4人でテキサスホールデムをする際に、プリフロップで強い手札が来たので手持ちの5%のチップをベットしたが、フロップの段階では思惑が外れた結果として、依然強い手札であるために自身の勝利確率が20%であると評価できたとする。このとき、他のプレイヤーが手持ちのチップの15%になるまでレイズしてきたとする。このとき、あなたはどのように行動するだろうか?選択肢としては
- Foldして、5%のチップを損切する。
- Callして、+10%(15%)分のチップを投入する。
のいずれかだろう。おそらく、初心者プレイヤーの多くは2.を選択するのではないだろうか?思惑が外れたとはいえ、まだ20%も勝利確率があるのに、5%の損失を確定してしまうことをもったいないと感じるのである。期待値で見ても
\[ \small \begin{align*} &E[W_1] = 0.95 \\ &E[W_2] = 0.2 \times 1.45 + 0.8 \times 0.85 = 0.97 \end{align*} \]
であり、それは合理的だろうと思うかもしれない。この行動がなぜ不適切であるかというと、そもそもあなたのリスク回避度はリスク中立的(\(\small \gamma=0\))ではないだろうということである。この問題をKelly基準(これでも一般的な人のリスク回避度よりかなり低い)で考えると
\[ \small \begin{align*} &E[U(W_1)] = \ln(0.95) = -0.05129 \\ &E[U(W_2)] = 0.2 \times \ln(1.45) + 0.8 \times \ln(0.85) = -0.0557 \end{align*} \]
であり、Foldすることが正しい選択になる。
反対に、フロップ、ターン、リバーで思惑通りの共通カードが出た結果、あなたは勝利確率を80%と推定したとする。このとき、リバーのタイミングでどれだけの金額をベットすればよいだろうか?おそらく、多くの人は手持ちのチップの15%から20%ぐらいと考えるのではないだろうか?これは、平均的なリスク回避度\(\small \gamma=5\)の場合の結果である。一方で、Kelly基準に従うのであれば、
\[ \small p = \frac{np-1}{n-1} =\frac{4 \times 0.8 -1}{4-1} = 0.7333 \]
であり、手持ちのチップの70%近くをベットするべきとなる。要するに、このケースで15%から20%程度しかベットしないプレイヤーが前の例で損切しないということは、リスクに対する態度が一貫していないということを意味している。
まとめると、弱いプレイヤーにどのような傾向があるかというと
- 勝利確率や期待リターンが低い賭けについて、リスク回避度が低くなる(むしろリスク愛好的になる)。
- 勝利確率や期待リターンが高い賭けについて、リスク回避度が高くなる。
という問題を抱えていることが多いということである。人がなぜ宝くじを買うかということを考えれば、ギャンブルが好きな人ほどこの傾向があることは比較的容易に想像することができるだろう。テキサスホールデムでは、リスクに対する態度が一貫しているプレイヤーはリスク回避度の高低にかかわらず、強いプレイヤーである可能性が高いと筆者は推測する。そのため、NPCを弱体化するためには、リスク回避度を勝利確率\(\small p\)(あるいは、期待リターン\(\small p\alpha-c\))の関数として\(\small \gamma(p), \gamma'(p) > 0\)という形で表現すればよいということになる。この勝利確率に対するリスク回避度の傾きの大きさをプレイヤーの弱さとして定義すれば、NPCの強さを表現することができるだろう。
具体的な関数形として、期待リターンが0である(\(\small p=c/\alpha\))ときのリスク回避度を\(\small \bar{\gamma}\)と表し、リスクに対する一貫性のなさをパラメータ\(\small \lambda\)で表すと
\[ \small \gamma(p, \alpha) = \max\left\{\bar{\gamma} + \lambda\left(p-\frac{c}{\alpha} \right), 0 \right\} \]
のように定義すれば、上記の考察のようにプレイヤーの弱さを\(\small \lambda\)で表すことができると考えられる。
客観確率と主観確率
リスクに対する態度が一貫していないことがプレイヤーとしての弱さを表すと説明したが、もう一つやはり勝利確率の推定について、慣れないプレイヤーは一定のバイアスを持っていると推測できる。負ける確率が高いときに負ける確率を低く評価する一方で、勝つ確率が高いときに勝つ確率を低く評価するという傾向である。これは行動経済学ではプロスペクト理論として知らている性質である。
具体例を示すと、期待リターンが0になる確率を\(\small p_e\)と表すとき、プレイヤーが自分の敗北確率を\(\small p_l=\delta p_e, 0\leq\delta\leq 1\)以下にはならないと推定するものと仮定する。反対に、自分が勝利する確率も\(\small p_u=1-p_l\)以上にならないと推定すると仮定しよう。すなわち、客観確率\(\small p \in [0, 1]\)に対して、主観確率は\(\small \xi\in [p_l, p_u]\)の範囲の値しかとらないと考える。このとき、
- \(\small p=0 \; \Rightarrow \; \xi=p_l\)
- \(\small p=p_e \; \Rightarrow \;\xi=p_e\)
- \(\small p=1 \; \Rightarrow \; \xi=p_u\)
が成り立つと仮定しよう。主観確率が客観確率に関する二次関数\(\small \xi(p)=ap^2+bp+c\)と表される場合、二次関数の係数は
\[ \small \begin{align*} &a = \frac{p_e(p_u-p_l-1)+p_l}{p_e(1-p_e)} = \frac{p_l(1-2p_e)}{p_e(1-p_e)} \\ &b = p_u-a-c \\ &c = p_l \end{align*} \]
と計算できる。例として、\(\small \delta = 0.8, p_e = 0.25\)である場合、客観確率に対する主観確率は以下のグラフのように表現される。
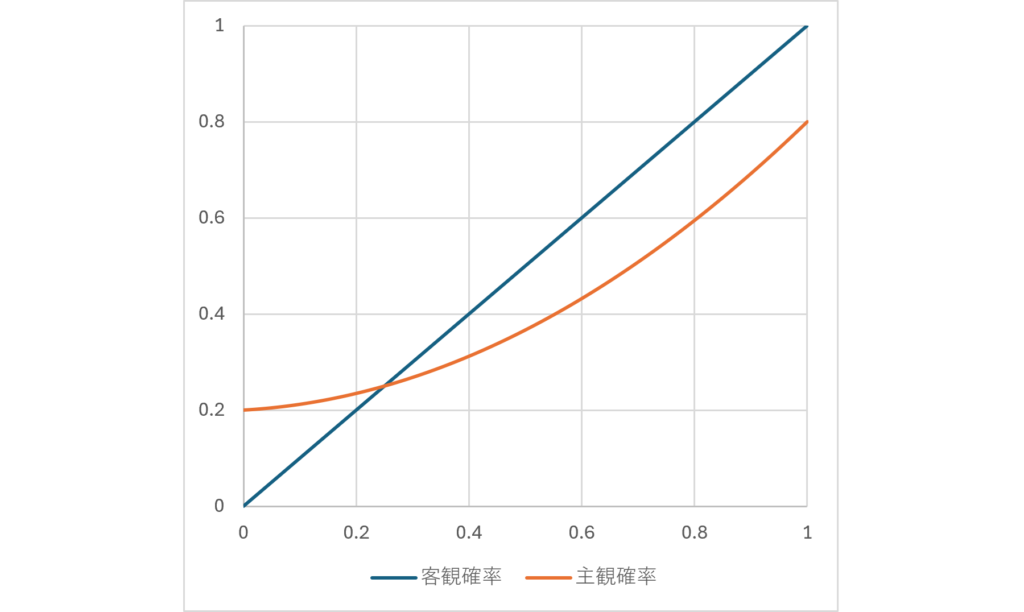
第3節で示したルースやタイトと言われるプレイヤーと異なり、確率のバイアスにも一貫性がないということがプレイヤーの弱さにつながっているということだろう。
テキサスホールデムにおけるプレイヤーの弱さの原因は客観確率を正しく評価できないことではなく、客観確率を正しく評価しているにも関わらず、主観確率で意思決定を行ってしまうことにある。人間の自然な感情に任せて賭けを行うと
- 勝利確率を客観確率ではなく主観確率で評価する。
- 期待リターンがマイナスのゲームでリスク愛好的になり、期待リターンがプラスのゲームでリスク回避的になる。
という性質が出てしまうために負けやすくなってしまうのだろう。コンピュータプログラムのNPCが強く感じるのは、これらの欠点とは無縁であるからである。人間のこういった傾向を直すためには、意識して相当の訓練を積まないと難しいのかもしれない。
NPCのパラメータのまとめ
以上の議論から、プレイヤーの性質を定めるパラメータは以下であると考えることができる。
- リスク回避度\(\small \bar{\gamma}\)
- スタイルパラメータ(\(\small s_p\), \(\small s_r\))
- 勝利確率に対するのリスク回避度の傾き\(\small \lambda\)、客観確率と主観確率の乖離\(\small \delta\)
これらのパラメータをユーザが保有するチップ(ユーザの強さ)に応じてやランダムに指定してNPCを追加していけばよいだろう。ここまでの内容で再びゲームを拡張してみた。
バランスの調整は必要だろうが、一応ゲームらしい体裁にはなってきたのではないだろうか。
ただし、実をいうとテキサスホールデムのプレイヤーとしてはまだ足りない要素がある。中級レベル以上のプレイヤーであれば、勝利確率推定のバイアスがないKelly基準で評価するプレイヤーを倒すことはそれほど難しいことではない(あるいは、不可能ではないだけでやはり難しい?)のかもしれない。これについては次回の投稿で説明することにする。




コメント