複素関数と時間

※ChatGPT画伯作 “A cyberpunk-inspired futuristic clock set in a high-tech cityscape.”

概要

　円錐座標系

\[ \small x^2+y^2+z^2+c^2T^2 = c^2t^2 \]

において、時空を

\[ \small \sqrt{x^2+y^2+z^2}+icT = cte^{i\theta}=c\zeta \]

と定義して

\[ \small c^2\zeta\zeta^{\ast} =x^2+y^2+z^2+c^2T^2 = c^2t^2 \]

と表現すると、この時空における時間の概念が

\[ \small \zeta = te^{i\theta} \]

で定義できるということを筆者は”複素関数とシュレディンガー方程式”で説明した。そして、光速度不変の原理を仮定する場合、これが逆行することを禁止した時間の概念になっているという主張を述べた。ただ、いまいち筆者はこの考え方を完全には理解していなかった（今も理解できていないけど）ように思える。もしかしたら、読者の中にも意味わからんと思っている人もいるかもしれないので、補足説明をしようというのが本稿の内容である。

時間は複素数平面（二次元空間）をらせん運動して進行する

　２次元平面\(\small R^2\)における等速円運動は

\[ \small \begin{align*} &x(t) = r\cos (\omega t) \\ &y(t) = r\sin (\omega t) \end{align*} \]

と表すことができる。これを複素数平面で表す場合は

\[ \small x(t)+y(t)i = re^{i\omega t} \]

と表現することできるだろう。複素数平面における等速円運動を表現するとこの式になる。

　円錐座標系における時間の概念は

\[ \small \zeta = t\exp\left(-i\frac{E}{\hbar} t\right) = t\exp\left(i\omega t\right) \]

であるから、２次元平面\(\small R^2\)におけるらせん運動に相当する。\(\small E>0,\omega<0\)では時計回りのらせん運動（左グラフ）、\(\small E<0,\omega>0\)では反時計回りのらせん運動（右グラフ）になる。具体的なグラフに表すと以下のとおりである。

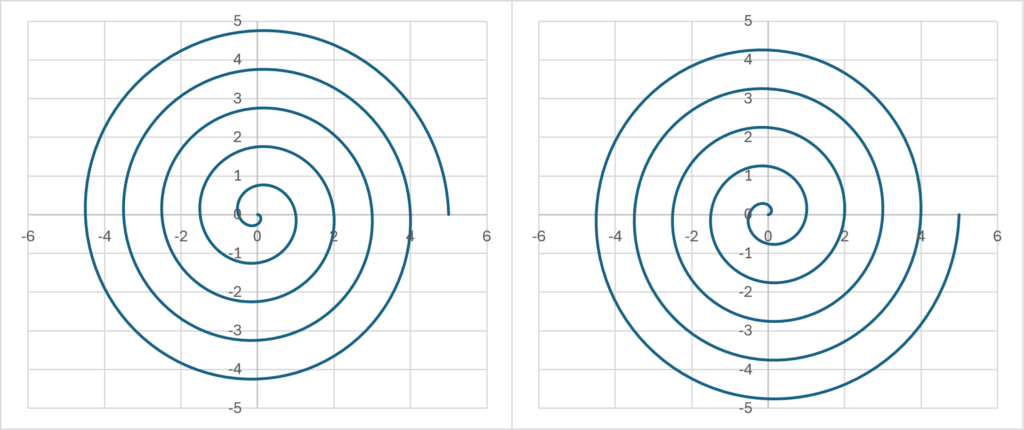
量子力学では、反時計回りに時間が進行する（すなわち、\(\small E<0\)である）量子を反粒子という。回転方向が反対なだけで時間を逆行しているわけではないことに注意する。現実に観測される時間が実数値のみであると仮定すれば、我々が時間として認識できるのは以下の赤丸でポイントした点のみを時間として認識しているということになる。我々が認識している時間は離散的であるということであり、このことが量子力学で観測される物理量が離散値になることの原因になっているという仮説を考えることもできるだろう。

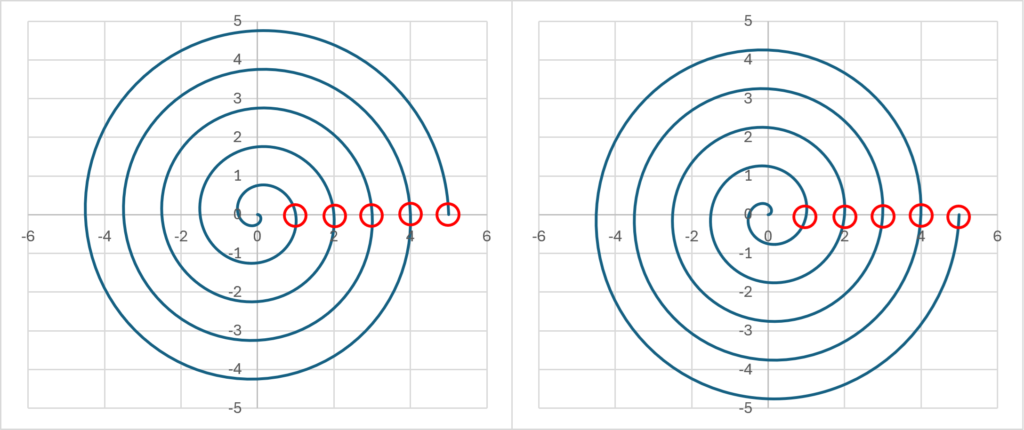
時間の長さ

　前節のように考えると、我々が認識している一定の速さで流れる時間\(\small \Delta t, 2\Delta t, \cdots\)に対して、物理的な時間の流れは異なったものであるかもしれないということになる。\(\small \Delta t\)の時間が経過する間に複素数の時間はらせん運動を1回転しているということであり、実際の時間の経過はこのらせん運動の経路長として計測しなければならないのかもしれない。以下の図で、色が異なる区間ごとで流れている時間の長さが異なっているということであり、これがどのような値になるかを計算してみよう。

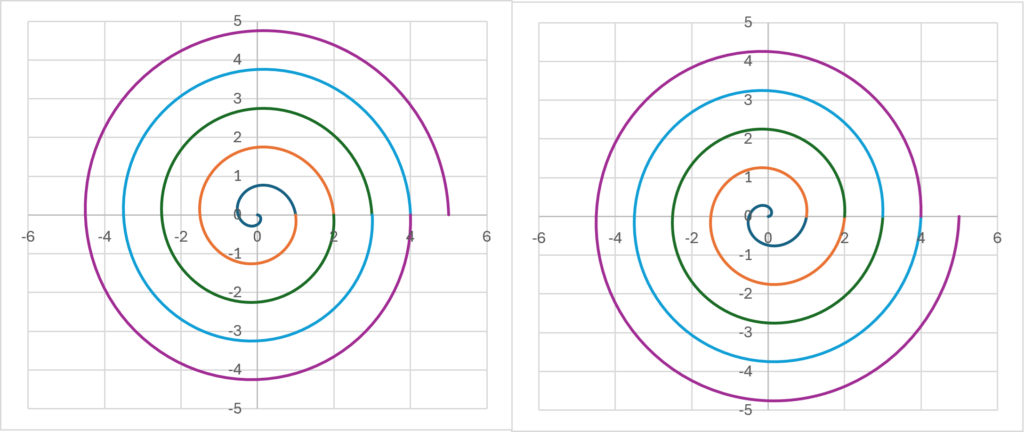
複素数平面を二次元のユークリッド空間とみなせば、時間\(\small \zeta(t)=te^{i\omega t}=x(t)+y(t)i\)は

\[ \small \begin{align*} &x(t) = t \cos \omega t \\ &y(t) = t \sin \omega t \end{align*} \]

と表すことができる。\(\small t\)について微分すると

\[ \small \begin{align*} &\frac{dx}{dt} = \cos\omega t – \omega t \sin \omega t \\ &\frac{dy}{dt} = \sin\omega t + \omega t \cos \omega t \end{align*} \]

を得る。時点\(\small t\)までの経路長は

\[ \small \int_0^t \sqrt{\left(\frac{dx}{du}\right)^2+\left(\frac{dy}{du}\right)^2} du \]

と計算することができる。

\[ \small \left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2 = 1+\omega^2t^2 \]

であるから

\[ \small T(t) = \int_0^t \sqrt{1 + \omega^2u^2} du \]

が経路長である。この積分を計算すると

\[ \small \begin{align*} \int_0^t \sqrt{1+\omega^2u^2}du & = \frac{1}{2\omega}\left(\omega t\sqrt{\omega^2t^2+1}+\sinh^{-1}(\omega t) \right) \\ & = \frac{1}{2\omega}\left(\omega t\sqrt{\omega^2t^2+1}+\log(\omega t+\sqrt{\omega^2t^2+1}) \right) \end{align*} \]

を得ることができる。

　我々が認識している離散的な時間の間隔を\(\small \Delta t\)と表して、区間\(\small [n\Delta t, (n+1)\Delta t]\)における経路長を計算しよう。正確な値は後で提示するものとして、ここでは次のように近似しよう。第２項は対数のオーダーなので無視して、\(\small \sqrt{\omega^2t^2+1} \approx \omega t\)と近似すると

\[ \small \int_{n\Delta t}^{(n+1)\Delta t} \sqrt{1+\omega^2u^2}du \approx \left[\frac{1}{2\omega}\omega^2t^2 \right]^{(n+1)\Delta t}_{n \Delta t} = \left(n + \frac{1}{2}\right)\omega\Delta t \]

を得ることができる。すなわち、我々が時間の経過を\(\small \Delta t, 2\Delta t, \cdots, n\Delta t\)と認識するのに対して、物理的な時間\(\small T(t)\)は

\[ \small \Delta T(t) = \left(n + \frac{1}{2}\right)\omega\Delta t \]

ずつだけ進行しているということになる。これは

\[ \small \frac{\Delta T(t)}{\Delta t} = \left(n+\frac{1}{2} \right)\omega \]

のように表すこともできるかもしれない。量子力学における電磁場（光）のエネルギーとこのことに何らかの関係があるのではないかというのが筆者が”複素関数とシュレディンガー方程式”において述べた仮説であった。

　ちなみに、上記の積分計算を厳密に行うと、正確に\(\small 1/2,3/2,5/2.\cdots\)とはならず軽微な誤差が生じることに注意する必要がある。実際に数値を示すと以下のとおりである（比較しやすいように\(\small \Delta T\)を\(\small 2n+1\)の形式にしている）。こういったズレが量子電磁気学で計算される補正値と関係がありそうであるが、現在の筆者には不明である。

n	ΔT
0	1.07685644147312
1	3.0174979418948
2	5.01025943726294
3	7.00728317754737
4	9.00565048878849
5	11.0046172791463
6	13.00390409145
7	15.0033820061521
8	17.0029832161817
9	19.0026686249351
10	21.0024140958786

参考文献

[1] 平野要 (2022), 多時間理論による量子力学ー二重スリット実験に関する一考察ー, Amazon Kindle Store（英語訳：Hirano, Kaname (2022), Quantum Mechanics with Multi-Time Theory, Amazon Kindle Store.）

[2] 平野要 (2024), 複素関数とシュレディンガー方程式, Amazon Kindle Store（英語訳：Hirano, Kaname (2024), Complex Functions and Schrödinger Equation, Amazon Kindle Store.）