概要
以前の投稿
で、回帰分析とニューラルネットワークを利用した機械学習の比較を行い、両者の差異について考察した。回帰分析のパラメータ推定に確率的勾配降下法という機械学習で良く用いられる手法を適用した場合にどのようになるかを示す。
線形回帰分析
データの数が\(\small n\)個、説明変数の数が\(\small m\)個の線形回帰モデルを考える。この場合、最小二乗法の問題は
\[ \small \min_{ \beta_1,\cdots,\beta_m } L( \beta_1,\cdots,\beta_m) = \min_{\beta_1,\cdots,\beta_m} \sum_{k=1}^n \left(y_k-\sum_{j=1}^m \beta_j x_{j,k} \right)^2 \]
と定式化できる。定数係数をモデルに含める場合は、\(\small x_{1,k} = 1, k=1,\cdots,n\)とおいて計算すればよいだろう。目的関数を説明変数で偏微分すると
\[ \small \frac{\partial L}{\partial \beta_j} = 2 \left( \sum_{l=1}^m \beta_l \sum_{k=1}^n x_{j,k} x_{l,k}-\sum_{k=1}^n x_{j,k} y_{k} \right) = 0 \]
であるから、行列の形で連立方程式を整理すると
\[ \small \left[ \begin{array}{llll} \displaystyle \sum_{k=1}^n x^2_{1,k} & \displaystyle \sum_{k=1}^n x_{1,k} x_{2,k} &\cdots& \displaystyle \sum_{k=1}^n x_{1,k} x_{m,k} \\ \displaystyle \sum_{k=1}^n x_{2,k} x_{1,k} & \displaystyle \sum_{k=1}^n x^2_{2,k} &\cdots& \displaystyle \sum_{k=1}^n x_{2,k} x_{m,k} \\ \qquad\vdots&\qquad\vdots&\ddots&\qquad\vdots \\ \displaystyle \sum_{k=1}^n x_{m,k} x_{1,k} & \displaystyle \sum_{k=1}^n x_{m,k} x_{2,k} &\cdots& \displaystyle \sum_{k=1}^n x^2_{m,k} \end{array} \right] \left[ \begin{array}{c} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_{m} \end{array} \right]=\left[ \begin{array}{c} \displaystyle \sum_{k=1}^n x_{1,k} y_{k} \\ \displaystyle \sum_{k=1}^n x_{2,k} y_{k} \\ \vdots \\ \displaystyle \sum_{k=1}^n x_{m,k} y_{k} \end{array} \right] \]
を得る。この連立一次方程式を解くことで回帰係数\(\small \beta_1, \cdots, \beta_m\)を推定することができる。この連立方程式は正規方程式(Normal Equation)といわれる。正規方程式はLU分解やガウスの掃き出し法などで解くと計算が発散しやすくなるため、特異値分解(SVD)という行列の計算法を用いて解くことが一般的である。
確率的勾配降下法
機械学習では、パラメータの推定は確率的勾配降下法(SGD: Stochastic Gradient Descent)といわれる手法で推定する。これはサンプルデータを一括で投入してパラメータを推定することはせずに、データをトレーニングセットと言われるいくつかの集合に分割して、そのトレーニングセットをランダムに繰り返し投入してパラメータを更新することで推定する手法である。データが投入されるごとにパラメータの推定値を更新する際のパラメータの更新式は\(\small n\)回目の更新後のパラメータが\(\small \hat{\beta}^{(n)}\)で与えられる場合、
\[ \small \hat{\beta}^{(n+1)}_j = \hat{\beta}^{(n)}_j-\eta\frac{\partial L\left(\hat{\beta}^{(n)},x^{(n+1)},y^{(n+1)}\right)}{\partial \beta_j} \]
と計算できる。\(\small \eta\)は学習率と言われるパラメータで外生的に与える。\(\small x^{(n+1)},y^{(n+1)}\)は\(\small n+1\)回目のトレーニングセットのデータを表す。\(\small L\)は損失関数といわれ、この関数を最小化するようにパラメータ\(\small \beta\)が推定されることになる。線形回帰モデルにおける損失関数は二乗誤差であり、前節で定義した\(\small L( \beta_1,\cdots,\beta_m)\)がそれに相当するため、偏微分係数は容易に計算することができる。
実際に、一変数の線形回帰分析で試してみると正しい解に収束していくことを見て取ることができるだろう。次のグラフは、\(\small y=2x+5+\epsilon, \epsilon\sim N(0,1)\)についてシミュレーション・パスを生成し、データを順番に学習させた場合のパラメータの推移である。学習率\(\small \eta\)は0.3に設定している。
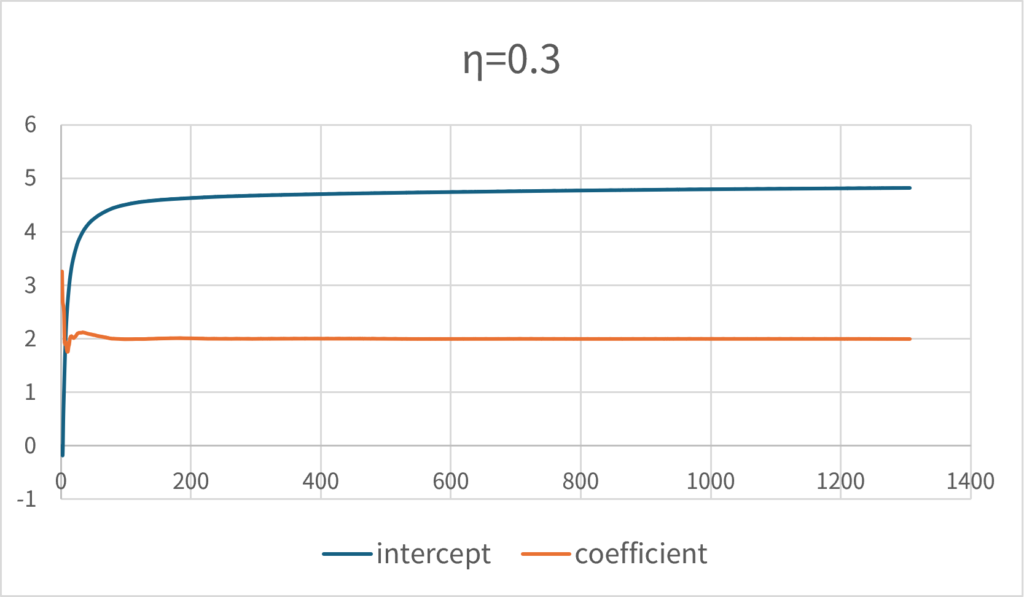
これは、学習率を低く設定すると著しく収束性が悪くなる。\(\small \eta=0.1\)とした場合は、同じ回数では正しい解には収束しない。
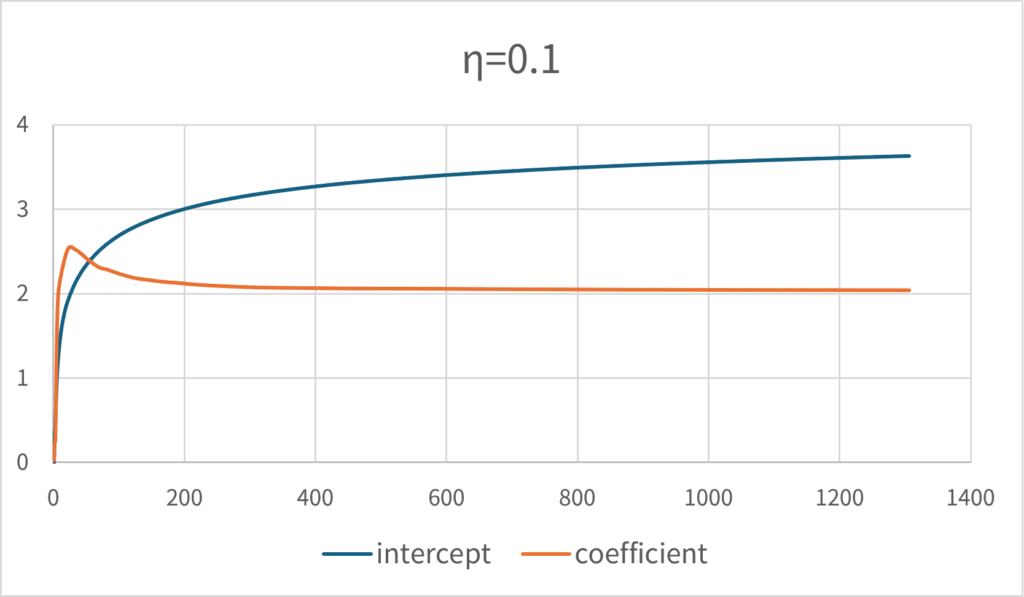
反対に学習率を高く設定しすぎると、解が発散しやすいことに注意する必要がある。\(\small \eta=1\)は最終的には正しい解近傍に収束しているが、初期の方では相当の程度でパラメータが暴れている様子が見て取れるだろう。
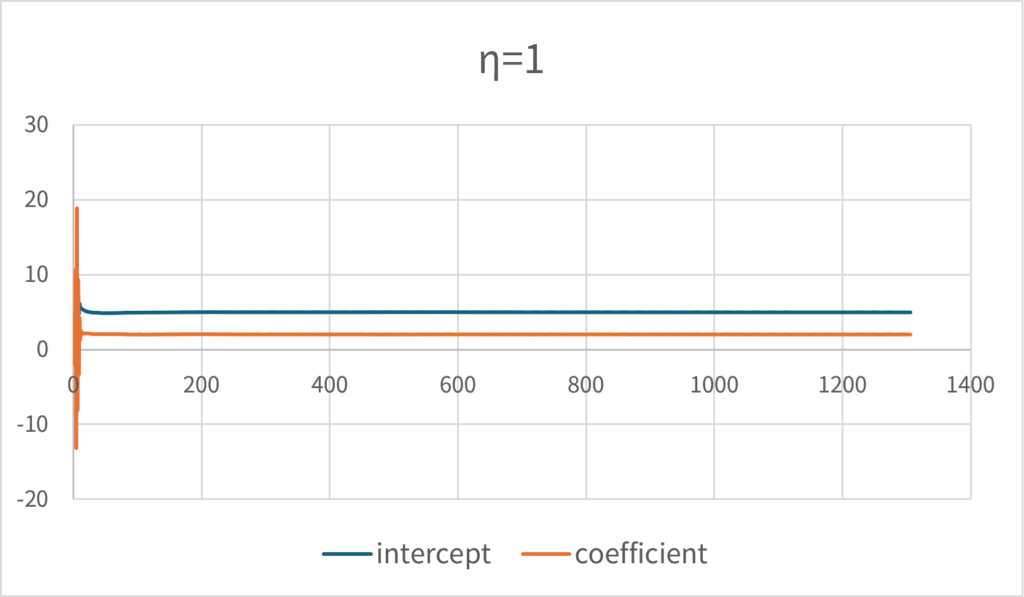
このアプローチはパラメータの数が多くなると収束性が悪くなるため、同じデータを使って繰り返しパラメータ更新を行う必要があり、それをランダムなデータセットで行うのが確率的勾配降下法のアルゴリズムということになる。学習率を高く設定すれば収束性は上がるが、解が発散してしまうリスクも高くなるということで、適切な値を設定する必要がある。この同じデータを繰り返し使ってパラメータの更新を行うという手続きが計算リソースを大量に要求する処理なのだろう。
オンライン機械学習
逐次的に観測されるデータを用いて、回帰モデルのパラメータを更新したいという場合がある。典型的には、時間の経過に伴ってモデルのパラメータが変化する傾向があるデータ(非定常な時系列データ)を分析する場合に、直近の観測値を反映するようにモデルのパラメータを推定するという問題である。このような場合は、一括で(オフラインで)推定処理を行って推定したパラメータを使い続けるのではなく、逐次的に学習データを投入してパラメータをオンラインで更新し続けるという手法を用いることになる。このような回帰分析や機械学習の手法はオンライン機械学習(Online Machine Learning)と言われる。
これを行う手法としては前節の確率的勾配降下法を用いる方法とカルマンフィルターを用いる再帰的最小二乗法(Recursive Least Squares)という方法があるらしい。確率的勾配降下法を用いる場合は、直近の観測データがサンプリングされる確率を高くするなどの工夫が必要になるだろう。カルマンフィルターを用いる方法はデータの分散共分散行列を計算しておき、それを基に最適なパラメータの遷移を推測する方法である。再帰的最小二乗法は計算の過程で、逆行列の計算が必要になるため、この逆行列を効率的に近似できる手法がない場合は、再度通常の回帰分析をやり直すことと計算コストが変わらないことに注意する必要がある。
回帰分析のこういった計算手法はあまり一般には知られていないように思う。現実にはよほどパラメータが多い回帰モデルでない限り、パラメータの推定に必要な処理は正規方程式(連立方程式)を一回解くだけであるため、適切なデータを選択して一括でパラメータを再計算した方が計算処理は速いようである。線形回帰分析に確率的勾配降下法を用いたり、再帰的最小二乗法といった手法が一般に知られていない理由は、現実には使い道があまりないからだろう。



