オイラー法
初期条件付きの常微分方程式
\[ \small \frac{dx}{dt} = f(x,t),\quad x(0) = x_0 \]
が与えられたとき、数値的にこの方程式の解を求める方法を考える。最も単純な方法は時間について離散化して計算する方法だろう。\(\small t_k = k\Delta t, \Delta t = 1/n,x_k=x(t_k)\)と置いて
\[ \small \frac{x_{k+1}-x_k}{\Delta t} = f(x_k, t_k) \]
と差分近似すれば
\[ \small x_{k+1} = x_k+f(x_k,t_k)\Delta t \]
と逐次計算することで解を求めることができる。これはオイラー法といわれる常微分方程式の数値解法である。
オイラー法は連立微分方程式に適用することもできる。
\[ \small \begin{align*} &\frac{dx}{dt} = f(x,y,t),\quad x(0) = x_0 \\
&\frac{dy}{dt} = g(x,y,t),\quad y(0) = y_0 \end{align*} \]
である場合は
\[ \small \begin{align*} &x_{k+1} = x_k+f(x_k,y_k,t_k)\Delta t \\
&y_{k+1} = y_k+g(x_k,y_k,t_k)\Delta t \end{align*} \]
と解けばよいだろう。
2階微分方程式の場合にも容易に拡張できて、
\[ \small \frac{d^2x}{dt^2} = f(x,t)\frac{dx}{dt}+ g(x,t),\quad x(0) = x_0,\;\frac{dx}{dt}(0) = v_0 \]
と表せる場合、
\[ \small \begin{align*} &\frac{dv(x,t)}{dt} = f(x, t)v(x,t)+g(x, t) \\ &\frac{dx(t)}{dt} = v(x,t) \end{align*} \]
と変形することができる。したがって、
\[ \small \begin{align*} &v_{k+1} = v_k+(f(x_k,t_k)v_k+g(x_k,t_k))\Delta t \\ &x_{k+1} = x_k + v_{k} \Delta t \end{align*} \]
で逐次計算すれば解を求めることができる。
例えば、重力の計算における連立微分方程式
\[ \small \begin{align*} &\frac{d^2x}{dt^2} = -\frac{GM}{r^3}x \\ &\frac{d^2y}{dt^2} = -\frac{GM}{r^3}y \\ &\frac{d^2z}{dt^2} = -\frac{GM}{r^3}z \end{align*} \]
は、オイラー法て計算すれば
\[ \small \begin{align*} &v_{x,k+1} = v_{x,k}-\frac{GMx_k}{\sqrt{x_k^2+y_k^2+z_k^2}^3}\Delta t \\ &v_{y,k+1} = v_{y,k}-\frac{GMy_k}{\sqrt{x_k^2+y_k^2+z_k^2}^3}\Delta t \\ &v_{z,k+1} = v_{z,k}-\frac{GMz_k}{\sqrt{x_k^2+y_k^2+z_k^2}^3}\Delta t \\ &x_{k+1} = x_k + v_{x,k} \Delta t \\ &y_{k+1} = y_k + v_{y,k} \Delta t \\ &z_{k+1} = z_k + v_{z,k} \Delta t \end{align*} \]
と計算することができる。
ルンゲ・クッタ法
オイラー法を使えば、容易に常微分方程式の解を求めることができる。しかし、オイラー法は計算精度が低く、相当の程度で時間幅を短くしても計算誤差が大きく発生することがある。実際に重力の計算における連立微分方程式などを実装してみれば、楕円軌道を描くものの1周して戻ってきたときに座標がずれているという事象が生じることは容易に確認できるだろう。計算精度を改善した手法として知られるのがルンゲ・クッタ法と言われる数値解法である。ここでは、ルンゲ・クッタ法の一般論の説明は避けて、簡単に使用できる計算方法のみを紹介しよう。
オイラー法に計算誤差が生じやすい原因は差分近似を一次のオーダーのみで行っているためであり
\[ \small dx = f(x, t)dt + \frac{1}{2}\left(\frac{\partial f(x,t)}{\partial t}+\frac{\partial f(x,t)}{\partial x}\frac{dx}{dt}\right)dt^2 \]
のように二次のオーダーまで考慮することで計算精度を上げることができるかもしれない。これは以下の計算方法で求めることができる。
\[ \small \begin{align*} &\xi_1 = f(x_k, t_k) \Delta t \\ &\xi_2 = f\left(x_k+\frac{1}{2}\xi_1, \;t_k+\frac{1}{2}\Delta t\right) \Delta t \\ &x_{k+1} = x_{k} + \xi_2 \end{align*} \]
ネストしている関数を線形近似すれば
\[ \small \begin{align*} x_{k+1} &= x_{k} + f\left(x_{k}+\frac{1}{2}f(t_k,x_k) \Delta t, \;t_k+\frac{1}{2}\Delta t\right)\Delta t \\ &\approx x_{k} + f(x_k, t_k)\Delta t + \frac{1}{2}\frac{\partial f(x_k,t_k)}{\partial t}\Delta t^2+ \frac{1}{2}\frac{\partial f(x_k,t_k)}{\partial x} f(x_k,t_k)\Delta t^2 \end{align*} \]
となっていることは理解できるだろう。これは二次のルンゲ・クッタ法といわれる常微分方程式の解法である。
さらに計算精度を上げるため
\[ \small \begin{align*} &\xi_1 = f(x_k, t_k) \Delta t \\ &\xi_2 = f\left(x_k+\frac{1}{2}\xi_1, \;t_k+\frac{1}{2}\Delta t\right) \Delta t \\ &\xi_3 = f\left(x_k+\frac{1}{2}\xi_2, \;t_k+\frac{1}{2}\Delta t\right) \Delta t \\ &\xi_4 = f\left(x_k+\xi_3, \;t_k+\Delta t\right) \Delta t \\ &x_{k+1} = x_{k} + \frac{1}{6}(\xi_1+2\xi_2+2\xi_3+\xi_4) \end{align*} \]
と計算する方法もあり、四次のルンゲ・クッタ法といわれる。これらの方法は二階の微分方程式にも容易に拡張できて
\[ \small h(x_k,v_k,t_k) = f(x_k,t_k)v_k+g(x_k,t_k) \]
と表すと
\[ \small \begin{align*} &\begin{array}{ll} \phi_1 = v_k\Delta t, &\quad \xi_1 = h(x_k,v_k,t_k)\Delta t \\ \phi_2 = \left(v_k+\frac{1}{2}\xi_1\right)\Delta t, &\quad \xi_2 = h\left(x_k+\frac{1}{2}\phi_1,v_k+\frac{1}{2}\xi_1,t_k+\frac{1}{2}\Delta t\right)\Delta t \\ \phi_3 = \left(v_k+\frac{1}{2}\xi_2\right)\Delta t,& \quad \xi_3 = h\left(x_k+\frac{1}{2}\phi_2,v_k+\frac{1}{2}\xi_2,t_k+\frac{1}{2}\Delta t\right)\Delta t \\ \phi_4 = \left(v_k+\xi_3\right)\Delta t, &\quad \xi_4 = h\left(x_k+\phi_3,v_k+\xi_3,t_k+\Delta t\right)\Delta t \end{array}\\ &v_{k+1} = v_{k} + \frac{1}{6}(\xi_1+2\xi_2+2\xi_3+\xi_4) \\ &x_{k+1} = x_{k} + \frac{1}{6}(\phi_1+2\phi_2+2\phi_3+\phi_4) \end{align*} \]
のように計算すればよいだろう。二次のルンゲ・クッタ法の場合は
\[ \small \begin{align*} &v_{k+1} = v_{k} + \xi_2 \\ &x_{k+1} = x_{k} + \phi_2 \end{align*} \]
と計算できる。だんだん微分方程式が解けない問題になりつつあるので、数値解法で対応できるものについてはこれで対応していくつもりである。
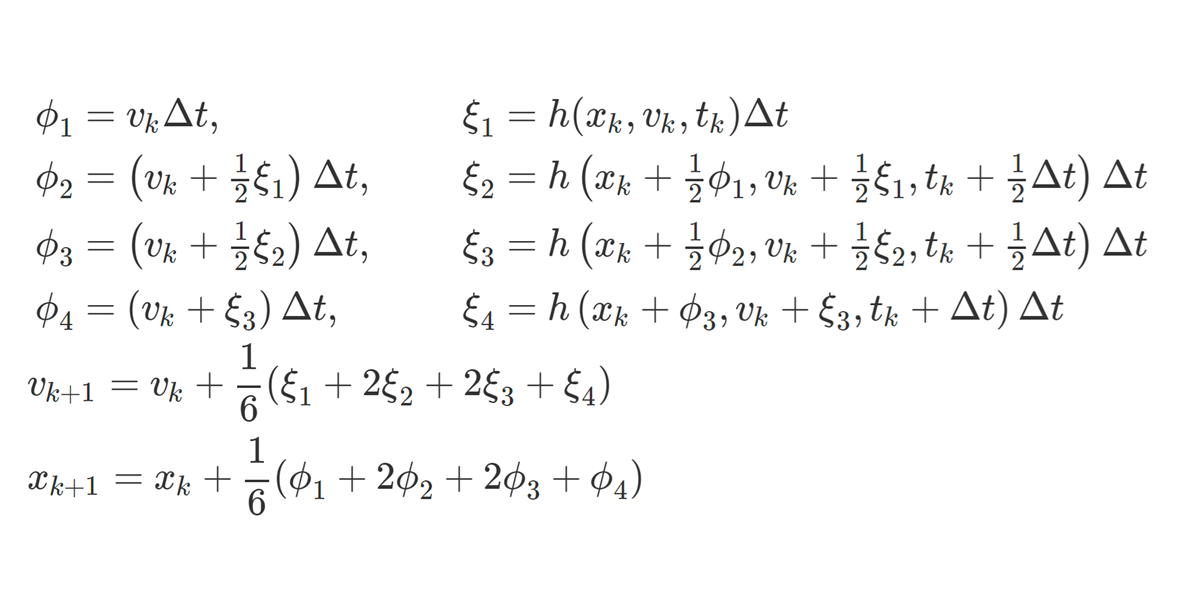


コメント