合成関数の確率分布
本題に入る前に、乱数\(\small x\)が確率密度関数\(\small p_f(x)\)に従うときに、連続関数\(\small y=g(x)\)で写像した値が従う確率分布の確率密度関数は
\[ \small p_g(y) = p_f(g^{-1}(y))\frac{dg^{-1}(y)}{dy} \]
で計算できることに注意する。証明は確率論や統計学の教科書に大抵載っている。以前の投稿で\(\small y=g(x)=\sqrt{x}\)が従う確率分布が
\[ \small p_g(x) = p_{x^2}(x^2)\frac{dg^{-1}(x)}{dx} = p_{x^2}(x^2)\frac{dx^2}{dx}=2xp_{x^2}(x^2) \]
に従うと書いたが、これを一般的な関数に拡張した結果である。
1次元球面の場合
二つの標準正規乱数\(\small x,y\sim N(0,1)\)が与えられたとき
\[ \small \begin{align*} &\hat{x} = \frac{x}{\sqrt{x^2+y^2}} \\ &\hat{y} = \frac{y}{\sqrt{x^2+y^2}} \ \end{align*} \]
が従う確率分布を考える。変数変換などを用いて計算すれば、これらの確率分布を求めることができるかもしれないが、意外に難しいかもしれない(ちなみに筆者は計算できなかった・・)。しかし、\(\small \hat{x}^2+\hat{y}^2=1\)であり、かつ、\(\small \hat{x},\hat{y}\)は球対称であるから、
\[ \small \begin{align*} &\hat{x} = \cos \eta \\ &\hat{y} = \sin \eta, \quad \eta\sim U[0,2\pi] \end{align*} \]
と計算した場合と等価な結果になると推測できる。\(\small U\)は一様分布を表す。逆三角関数の定義域は\(\small [-1,1]\)であるから、\(\small \hat{x}\)の確率密度関数は
\[ \small p(\hat{x}) = \frac{\frac{d\cos^{-1}\hat{x}}{d\hat{x}}}{\int_{-1}^1\frac{d\cos^{-1}\hat{x}}{d\hat{x}}dx} = \frac{1}{\pi \sqrt{1-\hat{x}^2}} \]
と求めることができる。実際に、モンテカルロシミュレーションなどで試せば、この結果が正しいことを確認できる。また、\(\small \hat{x},\hat{y}\)の共分散を計算すると
\[ \small E[\hat{x}\hat{y}] =\frac{1}{2\pi}\int_0^{2\pi}\sin\eta\cos\eta d\eta = 0 \]
であるから、\(\small \hat{x},\hat{y}\)の相関係数は0であることが分かる。
2次元球面の場合
同様にして、三つの標準正規乱数\(\small x,y,z\sim N(0,1)\)が与えられたとき
\[ \small \begin{align*} \hat{x} = \frac{x}{\sqrt{x^2+y^2+z^2}} \\ \hat{y} = \frac{y}{\sqrt{x^2+y^2+z^2}} \\ \hat{z} = \frac{z}{\sqrt{x^2+y^2+z^2}} \end{align*} \]
が従う確率分布を考える。これも定義域が\(\small [-1,1]\)であるが、球対称である(座標軸を交換しても確率分布は変わらない)ため、極座標を用いて
\[ \small \begin{align*} &\hat{x} = \sin \varphi \cos \eta \\ &\hat{y} = \sin \varphi \sin \eta \\ &\hat{z} = \cos \varphi, \qquad \quad \varphi\sim F(\varphi), \quad \eta\sim U[0,2\pi] \end{align*} \]
と表すことができる。ここで、\(\small F(\varphi)\)は確率密度関数と確率分布関数がそれぞれ
\[ \small \begin{align*} &p_F(\varphi) = \frac{1}{2}\sin \varphi \\ &F(\varphi) = \int p_F(\varphi)d\varphi = \frac{1}{2}(1-\cos \varphi), \quad \varphi \in[0,\pi] \end{align*} \]
である確率分布である。球対称であるのだから、\(\small \hat{z}\)の確率分布を求めればよい。
\[ \small p(\hat{z}) = \frac{\frac{1}{2}\sin\cos^{-1} \hat{z} \frac{d\cos^{-1} \hat{z}}{d\hat{z}}}{\int_{-1}^1\frac{1}{2}\sin\cos^{-1} \hat{z} \frac{d\cos^{-1} \hat{z}}{d\hat{z}}{d\hat{z}}} = \frac{1}{2} \]
であり、確率密度関数が定数になるので\(\small \hat{z}\)の確率分布は一様分布\(\small U[-1,1]\)であることが分かる。球対称であるから\(\small \hat{x},\hat{y}\)についても同様に一様分布に従うということになる。
3次元球面の場合
同様にして、四つの標準正規乱数\(\small x,y,z,s\sim N(0,1)\)が与えられたとき
\[ \small \begin{align*} &\hat{x} = \frac{x}{\sqrt{x^2+y^2+z^2+s^2}} \\ &\hat{y} = \frac{y}{\sqrt{x^2+y^2+z^2+s^2}} \\ &\hat{z} = \frac{z}{\sqrt{x^2+y^2+z^2+s^2}} \\ &\hat{s} = \frac{s}{\sqrt{x^2+y^2+z^2+s^2}} \end{align*} \]
が従う確率分布を考える。これも定義域が\(\small [-1,1]\)であるが、球対称である(座標軸を交換しても確率分布は変わらない)ため、極座標を用いて
\[ \small \begin{align*} &\hat{x} = \sin \theta \sin \varphi \cos \eta \\ &\hat{y} = \sin \theta \sin \varphi \sin \eta \\ &\hat{z} = \sin \theta \cos \varphi \\ &\hat{s} = \cos \theta, \qquad \quad \theta\sim G(\theta), \quad\varphi\sim F(\theta), \quad \eta\sim U[0,2\pi] \end{align*} \]
と表すことができる。ここで、\(\small G(\theta)\)は確率密度関数と確率分布関数がそれぞれ
\[ \small \begin{align*} &p_G(\theta) = \frac{2}{\pi}\sin^2 \theta \\ &G(\theta) = \int p_G(\theta)d\theta = \frac{1}{\pi}(\theta-\sin \theta\cos \theta), \quad \theta \in[0,\pi] \end{align*} \]
である確率分布である。球対称であるのだから、\(\small \hat{s}\)の確率分布を求めればよい。
\[ \small p(\hat{s}) = \frac{\frac{2}{\pi}\sin^2\cos^{-1}\hat{s} \left(\frac{d\cos^{-1} \hat{s}}{d\hat{s}}\right)}{\int_{-1}^1\frac{2}{\pi}\sin^2\cos^{-1}\hat{s} \left(\frac{d\cos^{-1} \hat{s}}{d\hat{s}}\right){d\hat{s}}} =\frac{2}{\pi}\sqrt{1-\hat{s}^2} \]
が確率密度関数になる。球対称であるから\(\small \hat{x},\hat{y},\hat{z}\)についても同じ確率分布に従うということになる。ここまでくると\(\small n\)次元球面まで一般化できそうで
\[ \small p_n(\hat{x}) =\frac{(1-\hat{x}^2)^{\frac{n-2}{2}}}{\int_{-1}^1 (1-\hat{x}^2)^{\frac{n-2}{2}} d\hat{x}} \]
と推測できる。プログラムで試した感じではこの結果で正しそうに見える。
条件付確率分布
ここまで球対称な確率分布を扱ってきたが、興味があるのは一つの座標軸の値が正規乱数ではなく定数である場合である。例えば、3次元球面において\(\small s\)が定数であるという場合に\(\small \hat{x},\hat{y},\hat{z},\hat{s}\)の確率分布はどのようになるだろうか?\(\small \hat{s}\)方向のみ非対称な確率分布になるだろう。この場合の確率分布を計算してみよう。
例によって、1次元球面の例から考えよう。\(\small y=\bar{y}\)で値がすでに決まっていると仮定する。この場合における1次元球面上の座標
\[ \small \begin{align*} &\hat{x} = \frac{x}{\sqrt{x^2+\bar{y}^2}} \\ &\hat{y} = \frac{\bar{y}}{\sqrt{x^2+\bar{y}^2}}, \quad x\sim N(0,1) \end{align*} \]
の確率分布を計算する。\(\small \hat{x} = g(x)\)と置くと、逆関数は
\[ \small g^{-1}(\hat{x}) =\pm\frac{\hat{x}\bar{y}}{\sqrt{1- \hat{x}^2}} \]
である。したがって、
\[ \small p(\hat{x}|y=\bar{y}) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{\hat{x}^2\bar{y}^2}{2(1-\hat{x}^2)} \right)|\bar{y}|(1- \hat{x}^2)^{-\frac{3}{2}} \]
と計算できる。実際に計算してみると、以下のような関数になる。
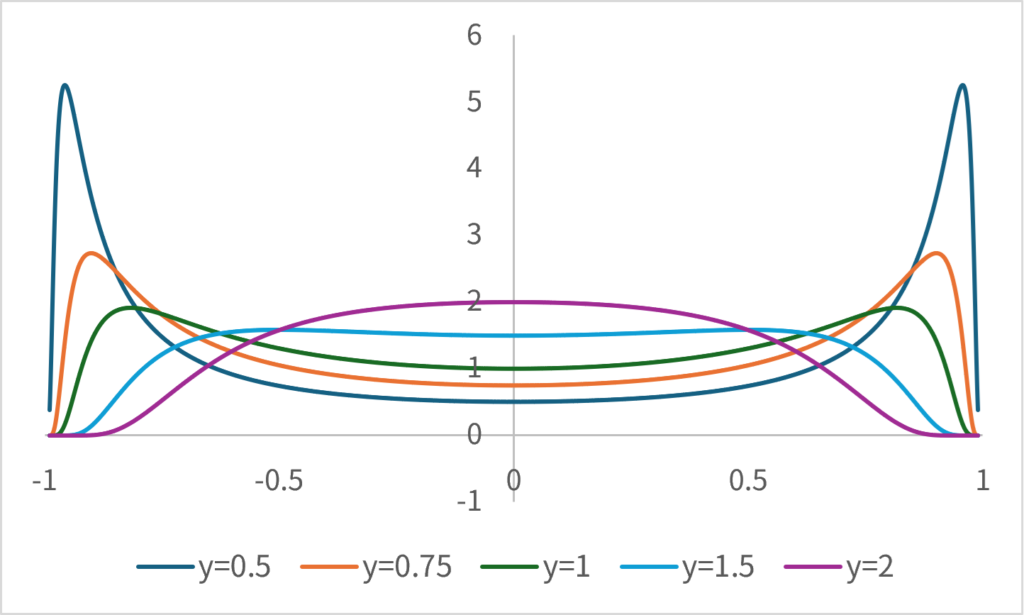
同様にして\(\small p(\hat{y})\)を求めると
\[ \small g^{-1}(\hat{y}) =\pm\frac{\bar{y}\sqrt{1-\hat{y}^2}}{\hat{y}} \]
であるから、
\[ \small p(\hat{y}|y=\bar{y}) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(1-\hat{y}^2)\bar{y}^2}{2\hat{y}^2} \right)\frac{|\bar{y}|}{\hat{y}^2\sqrt{1-\hat{y}^2}} \]
と計算できる。ただし、\(\small \bar{y}\)と\(\small \hat{y}\)は符号が同じ領域のみしか定義域が存在しない。実際に計算してみると、以下のような関数になる。
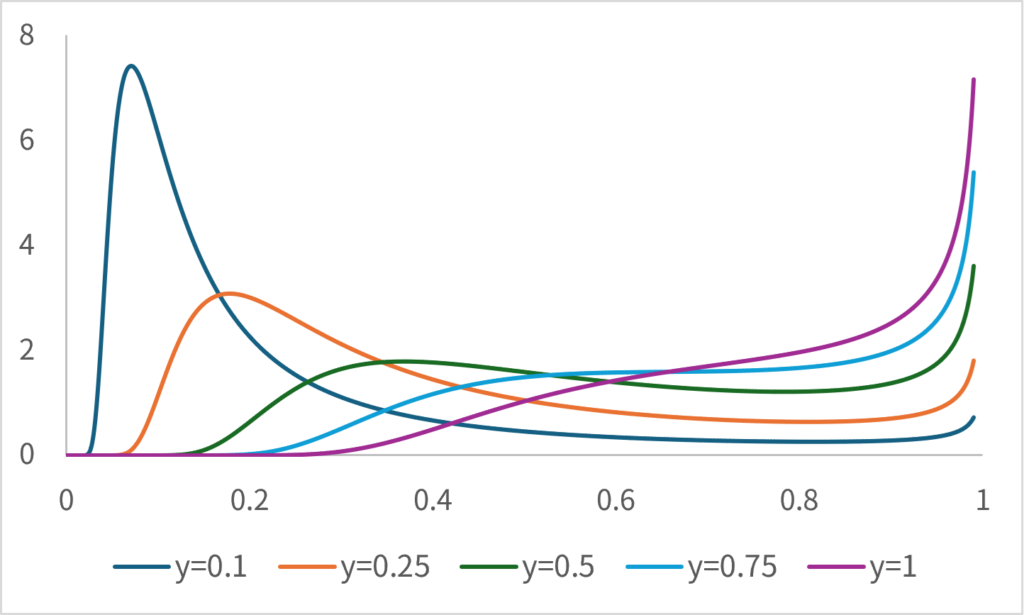
残念ながら、2次元以上の式を理論的に導出する方法が筆者にはわからない。ただ、モンテカルロシミュレーションの結果から以下が成り立つと推測できる。2次元と3次元の場合は
\[ \small \begin{align*} &p(\hat{x}|z=\bar{z}) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{\hat{x}^2\bar{z}^2}{2(1-\hat{x}^2)} \right)|\bar{z}|(1-\hat{x}^2)^{-3/4} \\ &p(\hat{x}|s=\bar{s}) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{\hat{x}^2\bar{s}^2}{2(1-\hat{x}^2)} \right)|\bar{s}| \ \end{align*} \]
である。ここから、\(\small n\)次元球面に拡張すると
\[ \small p_n(\hat{x}_j|x_n=\bar{x}_n, j=1,\cdots,n-1) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{\hat{x}_j^2\bar{x}_n^2}{2(1-\hat{x}_j^2)} \right)|\bar{x}_n|(1-\hat{x}_j^2)^{(n-3)3/4} \]
でありそうである。モンテカルロシミュレーションで試した結果は一般的な\(\small n\)について正しそうに見える。
非対称な座標軸については、モンテカルロシミュレーションの結果から
\[ \small \begin{align*} &p(\hat{z}|z=\bar{z}) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(1-\hat{z}^2)\bar{z}^2}{2\hat{z}^2} \right)\frac{|\bar{z}|}{\hat{z}^3} \\ &p(\hat{s}|s=\bar{s}) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(1-\hat{s}^2)\bar{s}^2}{2\hat{s}^2} \right)\frac{|\bar{s}|}{\hat{s}^4}(1-\hat{s}^2)^{\frac{1}{2}} \end{align*} \]
であると推測できる。\(\small n\)次元球面に拡張すると
\[ \small p_n(\hat{x}_n|x_n=\bar{x}_n) \propto \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(1-\hat{x}_n^2)\bar{x}_n^2}{2\hat{x}_n^2} \right)|\bar{x}_n|\hat{x}_n^{-(n+1)}(1-\hat{x}_n^2)^{(n-2)/2} \]
となる。エレガントな証明はそのうち考えたいけど、いまのところ想像もつかない・・・



コメント