問題の概要
前回の投稿
で、恒星の周りを運動する惑星などの軌道が楕円軌道であり、その運動方程式が
\[ \small \begin{align*} &r(t) = \frac{a(1-\epsilon^2)}{1+\epsilon \cos \omega(t)} \\ &x(t) = r(t)\cos \omega(t) \\ &y(t) = r(t)\sin \omega(t) \\ &z(t) = 0 \\ &\frac{d\omega}{dt} = \frac{|L|}{mr^2} \end{align*} \]
であることを示した。ここで、\(\small a\)は長半径、\(\small \epsilon\)は離心率、
\[ \small |L| = \sqrt{L^2} = \sqrt{Gm^2Ma(1-\epsilon^2)} \]
は軌道角運動量である。等速円運動と異なり、\(\small \omega(t)\)は一定の速度とすることができず、微分方程式
\[ \small \frac{d\omega}{dt} = \frac{|L|}{mr^2} = \sqrt{GM}\frac{(1+\epsilon \cos \omega(t))^2}{a^{3/2}(1-\epsilon^2)^{3/2}} \]
を満たさなければならないのであった。この微分方程式の解を求め、時間に対する楕円軌道を正確に特定しようというのが本稿が扱う問題である。
ケプラー方程式
微分方程式を解く代わりにケプラー方程式といわれる代数方程式を解くことで解を求める方法を考えよう。これを説明するためには、いくばくかややこしい概念を説明する必要がある。端的に示せば、以下の図のとおりである。
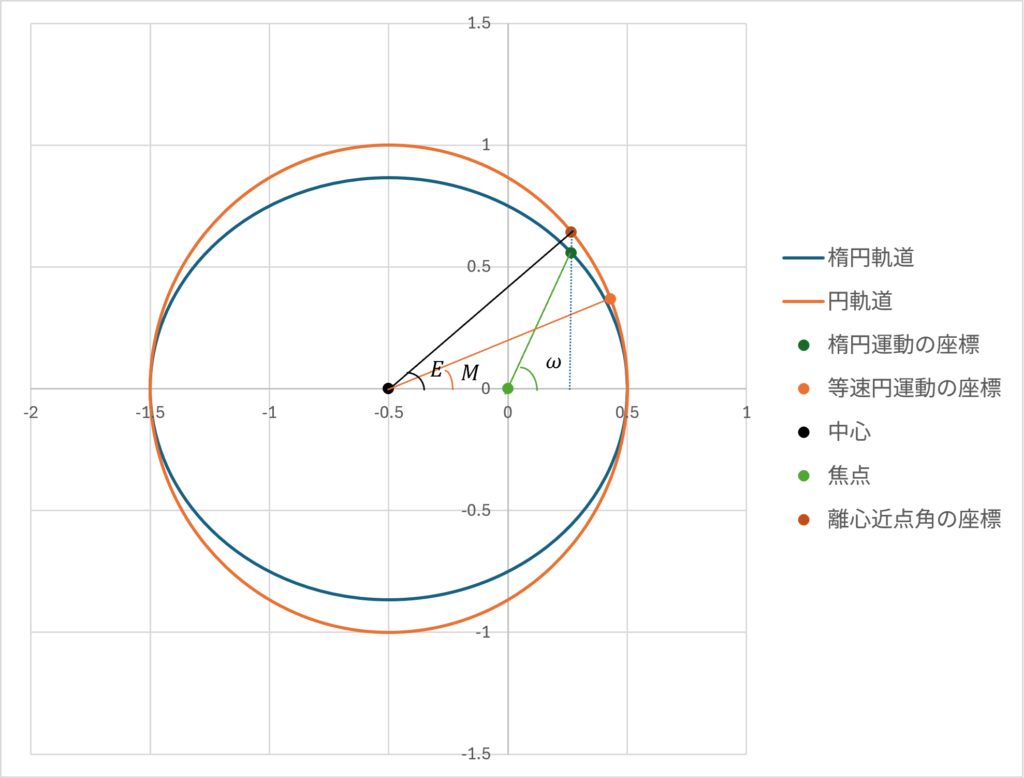
\(\small \omega(t)\)と書いていた値は楕円運動の焦点と座標が\(\small x\)軸に対してなす角度を表すパラメータであり、真近点角(True Anomaly)という。焦点の代わりに楕円運動の中心と座標、及び、楕円運動の\(\small y\)軸の値を円運動に直線で伸ばした座標が\(\small x\)軸に対してなす角度\(\small E(t)\)も定義することができて、離心近点角(Eccentric Anomaly)という。楕円運動との比較として、同じ周期\(\small T\)を持つ等速円運動を考えて、楕円運動の中心とその等速円運動の座標が\(\small x\)軸に対してなす角度\(\small M(t)\)を平均近点角(Mean Anomaly)という。定義から
\[ \small M(t) = 2\pi\frac{t}{T} \]
と表すことができる。\(\small \omega(t)\)が楕円運動における座標に対しての角度であるのに対して、\(\small E(t),M(t)\)は円運動上の座標に対しての角度であることに注意する。
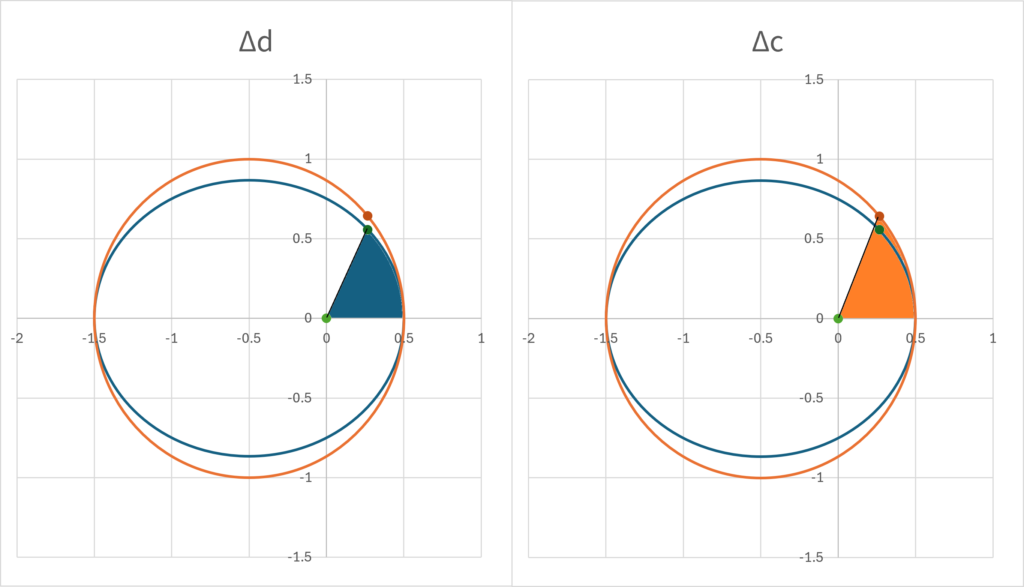
それぞれの角度や軌道半径との関係式を求めよう。楕円運動と等速円運動は面積速度がいずれも一定であるから、時点\(\small t\)までに掃いた面積と軌道が囲む面積の比は同一でなければならない。また、角度\(\small \omega(t)\)が形成する扇形の楕円に対して占める面積と離心近点角の座標が形成する扇形の円に対して占める面積の比率は同じ値でなければならない。すなわち、焦点と\(\small x\)軸、楕円運動の座標と離心近点角の座標が囲む扇型の面積を\(\small \Delta d, \Delta c\)とすれば
\[ \small \frac{M(t)}{2\pi} = \frac{\Delta d}{\pi a b} = \frac{\Delta c}{\pi a^2} \]
が成り立つ。ここで、\(\small b=a\sqrt{1-\epsilon^2}\)は楕円の短半径を表す。
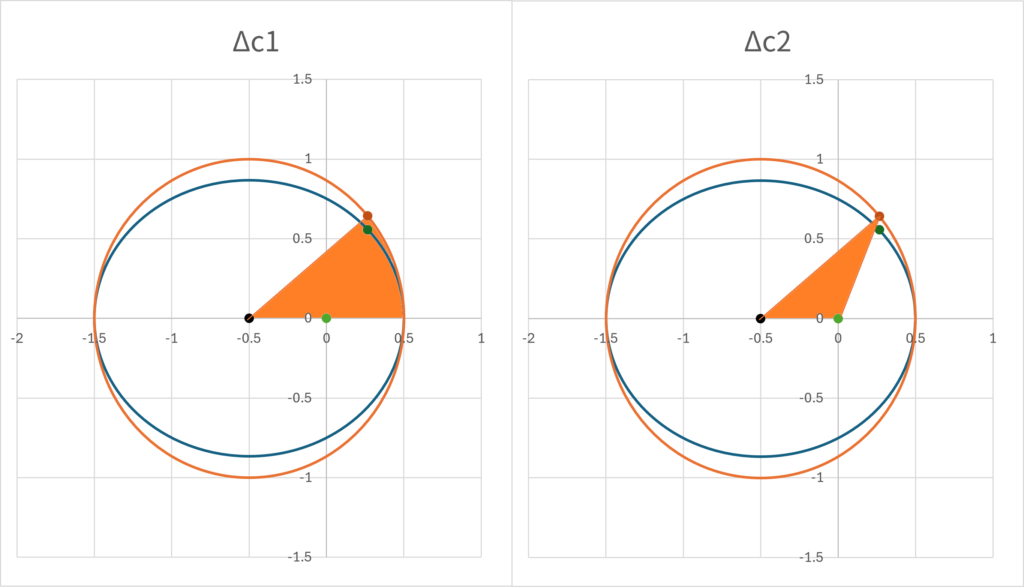
\(\small \Delta c\)を求めるためには、中心と\(\small x\)軸、離心近点角の座標が囲む扇型の面積から中心と焦点、離心近点角の座標が囲む三角形の面積を引けばよい。扇型の面積は円の面積\(\small \pi a^2\)に中心角を掛けた値であるから、
\[ \small \Delta c_1 = \frac{1}{2}a^2E(t) \]
三角形の面積は、中心と焦点の距離は\(\small a\epsilon\)、縦の長さが\(\small a\sin E(t)\)であるから、
\[ \small \Delta c_2 = \frac{1}{2}(a\epsilon) a\sin E(t) \]
となる。したがって、
\[ \small M(t) = E(t)-\epsilon\sin E(t) \]
が成り立つ。この方程式はケプラー方程式といわれる代数方程式である。
また、楕円軌道の座標は離心近点角\(\small E(t)\)を用いて
\[ \small x(t)= a\cos E(t)-a\epsilon, \quad y(t) = a\sqrt{1-\epsilon^2} \sin E(t) \]
と表すことができる。これは、焦点と中心の距離が\(\small a\epsilon\)であること、及び、楕円の短い半径が\(\small b=a\sqrt{1-\epsilon^2}\)であることから確認できるだろう。したがって、
\[ \small r(t) = \sqrt{x^2(t)+y^2(t)} = a(1-\epsilon\cos E(t)) \]
を得る。この式から
\[ \small r(t) = \frac{a(1-\epsilon^2)}{1+\epsilon \cos \omega(t)} = a(1-\epsilon\cos E(t)) \]
であるから、\(\small \omega(t)\)と\(\small E(t)\)の関係を求めると
\[ \small \sin E(t) = \frac{\sqrt{1-\epsilon^2}\sin \omega(t)}{1+\epsilon \cos \omega(t)} \\ \small \sin \omega(t) = \frac{\sqrt{1-\epsilon^2}\sin E(t)}{1-\epsilon \cos E(t)} \]
となる。
ベッセル関数を利用した解法
ケプラー方程式
\[ \small M(t) = E(t)-\epsilon\sin E(t) \]
を\(\small E(t)\)について、\(\small M(t)\)の関数(すなわち、\(\small t\)の関数)として解く方法を考えよう。\(\small M(t)-E(t)\)は\(\small 2\pi\)の周期を持つことから、sin級数でフーリエ変換出来て
\[ \small E(t)-M(t) = \sum_{i=n}^\infty B_n \sin n M(t) \]
を得る。フーリエ係数はフーリエ逆変換をすると
\[ \small B_n = \frac{2}{\pi} \int_0^\pi (E(t)-M(t)) \sin n M(t) dM(t) \]
が成り立つ。部分積分をすると
\[ \small B_n = \frac{2}{\pi}\left(\left[ -(E(t)-M(t))\frac{\cos nM(t)}{n} \right]_{M(t)=0}^{M(t)=\pi}+\int_0^\pi \frac{\cos nM(t)}{n}(dE(t)- dM(t))\right) \]
となる。第1項は0であり、また
\[ \small \int_0^\pi \frac{\cos nM(t)}{n}dM(t) = 0 \]
である。したがって、
\[ \small \begin{align*} B_n &= \frac{2}{\pi n} \int_0^\pi \cos nM(t) dE(t) \\ &= \frac{2}{\pi n} \int_0^\pi \cos n(E(t)-\epsilon\sin E(t)) dE(t) \ \end{align*} \]
が成り立つ。\(\small x=n\epsilon\)と置いて、ベッセル積分の式
\[ \small J_n(x) = \frac{1}{\pi}\int_0^{\pi} \cos(n\theta-x\sin\theta)d\theta \]
と比較すれば
\[ \small B_n = \frac{2}{n}J_n(n\epsilon) \]
を得る。sin級数の式に代入すると
\[ \small E(t) = M(t)+2\sum_{i=n}^\infty \frac{J_n(n\epsilon)}{n} \sin nM(t) \]
がケプラー方程式の解になる。軌道半径は
\[ \small r(t) = a(1-\epsilon\cos E(t)) \]
であったから
\[ \small r(t) = a-a\epsilon \cos\left(M(t)+2\sum_{i=n}^\infty \frac{J_n(n\epsilon)}{n} \sin nM(t) \right) \]
と計算できる。\(\small \omega(t)\)は
\[ \small \cos \omega(t) = \frac{1}{\epsilon}\left(\frac{a(1-\epsilon^2)}{r(t)}-1\right) \]
から逆算し求めることができる。\(\small \cos^{-1}(x)\)は多価関数なので、適切な主値を選択する必要があることに注意する。このようにして計算した\(\small \omega(t)\)は微分方程式
\[ \small \frac{d\omega}{dt} = \frac{|L|}{mr^2} = \sqrt{GM}\frac{(1+\epsilon \cos \omega(t))^2}{a^{3/2}(1-\epsilon^2)^{3/2}} \]
の解であるということである。
周期を\(\small T=1\)と置いて、
\[ \small E(t) = 2\pi t+2\sum_{i=n}^\infty \frac{J_n(n\epsilon)}{n} \sin 2\pi nt \]
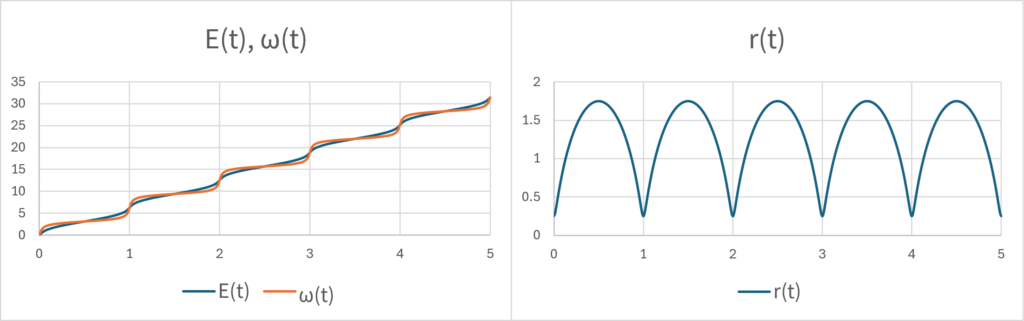
のとき、いくつかの\(\small 0<\epsilon<1\)について、\(\small E(t),r(t),\omega(t)\)のグラフを示すと以下のとおりである。

これらの変数は周期的な挙動をしており、\(\small t>1\)以降もつなげてグラフにすると以下のようになる。\(\small E(t),\omega(t)\)は\(\small t\)について単調増加関数であり、\(\small \omega(t)\)が最初に示した微分方程式を満たしそうであることは何となく確認できるだろう。
最後に、時間間隔を均等にした場合の座標をグラフとしてプロットすると以下のとおりである。焦点か離れるほど、速度が遅くなる傾向があることが確認できるだろう。

参考文献
[1] Bowman, Frank, Introduction to Bessel Functions, Dover Publication Inc., 1958. (日本語訳:フランク・ボウマン, ベッセル函数入門, 日新出版, 1963)
[2] Watson, George N., A Treatise on the Theory of Bessel Functions Second Edition, Cambridge University Press, 1944.



