ベッセル関数

　ベッセル関数についてその性質を簡単にまとめておく。ほぼBowman （1958）の第6章の要約である。将来的にケプラー方程式（楕円運動の方程式）や原子核に束縛された電子の運動を考察してみたいということで、それに必要そうな情報をまとめてみた。

ベッセル関数
修正ベッセル関数
ベッセル関数の級数
参考文献

ベッセル関数

　以下の無限級数で表される関数を0階の（第一種の）ベッセル関数という。

\[ \small \begin{align*} J_0(x) & = 1-\frac{x^2}{2^2} + \frac{x^4}{2^2\cdot4^2}-\frac{x^6}{2^2\cdot4^2\cdot6^2}\cdots \\ & = \sum_{m=0}^\infty \frac{(-1)^m}{m!\Gamma(m+1)}\left(\frac{x}{2}\right)^{2m} \end{align*} \]

ここで、\(\small \Gamma(x)\)はガンマ関数である。一般化して、

\[ \small \begin{align*} J_n(x) & = \frac{x^n}{2^nn!}\left(1-\frac{x^2}{2(2n+2)} + \frac{x^4}{2\cdot4(2n+2)(2n+4)}\cdots\right) \\ & = \sum_{m=0}^\infty \frac{(-1)^m}{m!\Gamma(m+n+1)}\left(\frac{x}{2}\right)^{2m+n} \end{align*} \]

と置いたのが\(\small n\)階のベッセル関数である。ベッセル関数の間には

\[ \small \begin{align*} &\frac{d}{dx}\left\{x^nJ_n(x) \right\} = x^n J_{n-1}(x) \\
&\frac{d}{dx}\left\{\frac{J_n(x)}{x^n} \right\} = – \frac{J_{n+1}(x)}{x^n} \end{align*} \]

という関係が成り立つ。これは

\[ \small \frac{dJ_n(x)}{dx} = J_{n-1}(x)-\frac{n}{x}J_n(x)= -J_{n+1}(x)+\frac{n}{x}J_n(x) \]

と表すこともできる。この式から

\[ \small \frac{dJ_n(x)}{dx} = \frac{J_{n-1}(x)-J_{n+1}(x)}{2} \]

を得る。ベッセル関数は以下の常微分方程式の解である。

\[ \small x^2\frac{d^2y}{dx^2} + x\frac{dy}{dx}+(x^2 – n^2)y = 0 \]

この微分方程式は\(\small n\)階のベッセル方程式といわれる。\(\small J_n(x)\)は以下の積分で表すこともでき、ベッセル積分といわれる。

\[ \small J_n(x) = \frac{1}{\pi}\int_0^{\pi} \cos(n\theta-x\sin\theta)d\theta= \frac{1}{2\pi}\int_0^{2\pi} \cos(n\theta-x\sin\theta)d\theta \]

ベッセル方程式は第一種のベッセル関数\(\small J_n(x)\)以外にも

\[ \small Y_n(x) = \frac{J_n(x) \cos n\pi-J_{-n}(x)}{\sin n\pi} \]

を解に持ち、この関数を第二種のベッセル関数（\(\small n\)が整数の場合は分子と分母が0になるので、極限を計算する必要がある。）という。ベッセル方程式の一般解は\(\small J_n(x)\)と\(\small Y_n(x)\)の線形結合で表される。

　実際にグラフを計算すると以下のようなイメージである。

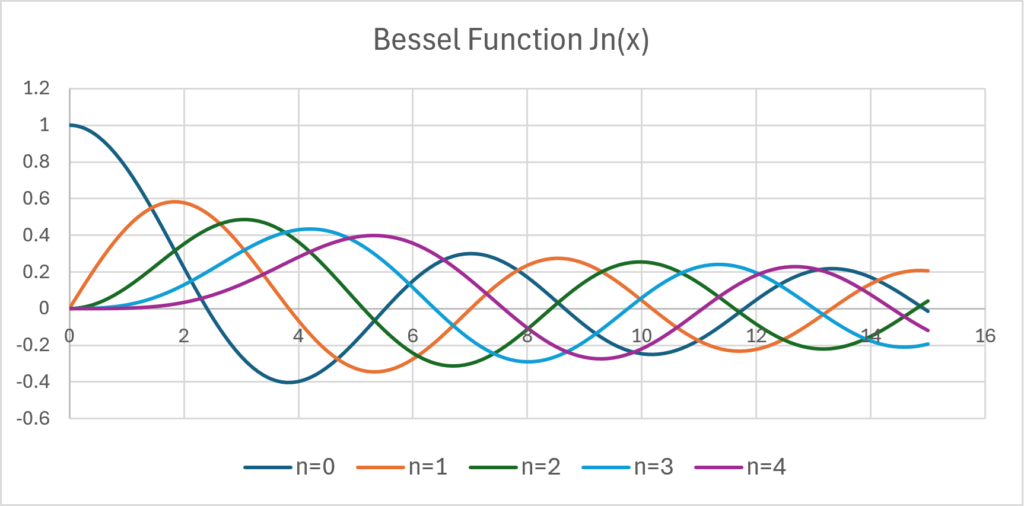
三角関数のように周期的な変動をすることが見て取れるだろう。

修正ベッセル関数

　ベッセル方程式を

\[ \small x^2\frac{d^2y}{dx^2} + x\frac{dy}{dx}-(x^2 + n^2)y = 0 \]

と修正した方程式の解を修正ベッセル関数という。これも2種類あり、それぞれ

\[ \small \begin{align*} &I_n(x) = i^{-n}J(ix) = \sum_{m=0}^\infty \frac{1}{m!\Gamma(m+n+1)}\left(\frac{x}{2}\right)^{2m+n} \\ &K_n(x) = \frac{\pi}{2}\frac{I_{-n}(x)-I_{n}(x)}{\sin n\pi} \end{align*} \]

と定義される（\(\small K_n(x)\)については、\(\small n\)が整数の場合は極限を計算する必要がある。）。元のベッセル関数と異なり指数関数のように単調に増加する関数である。

　もう一つの変形として

\[ \small x^2\frac{d^2y}{dx^2} + 2x\frac{dy}{dx}+(x^2 – n(n+1))y = 0 \]

の解を球ベッセル関数という。この形式は（何の問題か知らないけど）シュレディンガー方程式で登場する方程式であることは知られていることだろう。それぞれ

\[ \small j_n(x) = \sqrt{\frac{\pi}{2x}}J_{n+1/2}(x) \\
\small y_n(x) = \sqrt{\frac{\pi}{2x}}Y_{n+1/2}(x) \]

で定義される。

ベッセル関数の級数

　ベッセル関数に関する級数の計算は非常に多くの公式が存在するが、ここでは基本的なもののみ示す。

\[ \small \begin{align*} \exp\left(\frac{1}{2}x\left(t-\frac{1}{t} \right)\right) &= \sum_{n=-\infty}^\infty t^nJ_n(x) \\ & = J_0(x)+\sum_{n=1}^\infty (t^n+(-1)^nt^{-n})J_n(x) \end{align*} \]

この形式の指数関数についてTaylor展開の係数がベッセル関数に相当しているということである。\(\small t\)を\(\small e^{i\theta}\)と置き換えると

\[ \small \begin{align*} \exp\left(ix\sin\theta \right)&= J_0(x)+\sum_{n=1}^\infty (e^{in\theta}+(-1)^nt^{-in\theta})J_n(x) \\ &= J_0(x)+2\sum_{n=1}^\infty \cos(2n\theta)J_{2n}(x)+2i\sum_{n=0}^\infty \sin((2n+1)\theta)J_{2n+1}(x) \end{align*} \]

が成り立つ。これはJacobi展開というらしい。この式から以下の級数を得ることができる。

\[ \small \begin{align*} &\cos(x\sin\theta) = J_0(x)+2\sum_{n=1}^\infty \cos(2n\theta)J_{2n}(x) \\ &\sin(x\sin\theta) =2\sum_{n=0}^\infty \sin((2n+1)\theta)J_{2n+1}(x) \\ &\cos(x\cos\theta) = J_0(x)+2\sum_{n=1}^\infty (-1)^n\cos(2n\theta)J_{2n}(x) \\ &\sin(x\cos\theta) =2\sum_{n=0}^\infty (-1)^n\sin((2n+1)\theta)J_{2n+1}(x) \end{align*} \]

最後に、\(\small 0<x<1\)で定義された任意の関数\(\small f(x)\)は\(\small J_n(x)=0\)を満たす正の解を小さい順に\(\small \alpha_1,\alpha_2,\cdots\)と表すと

\[ \small \begin{align*} &f(x) = \sum_{i=1}^\infty A_iJ_n(x\alpha_i) \\ &A_i = \frac{2}{J_{n+1}^2(\alpha_i)}\int_0^1 xf(x)J_n(x\alpha_i)dx \end{align*} \]

と近似できる。これはフーリエ-ベッセル展開といわれるフーリエ展開の一種である。