問題の設定と解
電子の運動、すなわち、時間の進行によって電子が検出される確率分布がどのように変化するかはシュレディンガー方程式
\[ i \hbar\frac{\partial \psi(x,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \frac{\partial^2 \psi(x,t)}{\partial x^2}+V(x)\psi(x,t) \]
で記述される。特に、ポテンシャルが\(\small V(x)=0 \)である場合、すなわち、他の物理的な対象から影響を受けない状態を自由状態という。電子が他の量子と相互作用しない場合にどのように運動するかということであり、この場合における電子が検出される座標の確率分布がどのように変化するかをシュレディンガー方程式を解くことで求めてみよう。
一般に量子は座標について不確定性を持つと言われるが、自然な状態の確率分布を考えるのであれば正規分布に従った不確実性を持っていると考えるのが妥当な推測だろう。そのため、初期時点の量子の座標の確率分布が正規分布に従うものと仮定する。このような仮定のモデルはガウス型の波束モデル(Gaussian wave packet model)といわれている。量子力学の教科書(例えば、朝永振一郎『量子力学Ⅱ』)に従うと、初期状態の座標と運動量に対応する波動関数は以下で与えられる。
\[ \psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right) \]
ここで、\(\small \bar{p}\)は運動量の期待値、\(\small \sigma \)は観測される座標の不確実性を表すパラメータである。このとき、観測される座標の確率分布は正規分布に従っており、
\[ P(x,0)=|\psi(x,0)|^2 = \frac{1}{\sqrt{\pi\sigma^2}} \exp\left(-\frac{x^2}{\sigma^2}\right) \]
と書くことができる。
以上のことから、自由状態における電子の運動は基礎方程式と境界条件が
\[ \begin{align*} &i \hbar\frac{\partial \psi(x,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \frac{\partial^2 \psi(x,t)}{\partial x^2} \\ &\psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right) \end{align*} \]
であるときの\(\small \psi(x,t)\)を求めよ、という問題になる。”さあ、偏微分方程式の練習問題だ、とっとと解いて見せろ”と言われたとき、あなたはこの問題を解くことができるだろうか?先に解答を示すと(朝永振一郎『量子力学Ⅱ』から引用)
\[ \begin{align*} \psi(x,t) \; & = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left( x -\frac{\bar{p}}{m}t \right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{\hbar}x -\frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left( x -\frac{\bar{p}}{m}t \right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right) \ \end{align*} \]
が解である。地道に偏微分を計算して方程式に当てはめれば条件を満たしていることが確認できるだろう。したがって、
\[ \begin{align*} P(x,t) \; & = \psi^{\ast}(x)\psi(x) \\ &= \frac{1}{\sqrt{\pi} \sigma \left( 1+\left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)^{1/2}} \exp \left(- \frac{\left( x -\frac{\bar{p}}{m}t \right)^2}{\sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \end{align*} \]
が成り立つ。これは正規分布であり、\(\small N(\mu, \sigma^2)\)を正規分布関数とすると
\[ x(t) \sim N\left(\frac{\bar{p}}{m}t, \;\frac{\sigma^2}{2} + \frac{\hbar^2}{2m^2\sigma^2}t^2 \right) \]
が時点\(\small t\)における電子の観測座標の確率分布であることがわかる。おいおい、どうやってこれを導出したんだよ、というのが本稿の主題である。
導出
前節の解はフーリエ変換を用いて導出するようである。境界条件をフーリエ変換して
\[ \psi(x,0) = \int_{-\infty}^\infty A_k\exp(ikx) dk \]
と置く。これは、\(\small \psi_k(x,0)=\exp(ikx)\)という無数の複素関数の重ね合わせとして解を表現できるということを意味する。
\[ \frac{\partial \psi_k(x,t)}{\partial x} = ik\psi_k(x,t) \]
を仮定して、シュレディンガー方程式に代入すれば
\[ \frac{\partial^2 \psi_k(x,t)}{\partial x^2} = -k^2\psi_k(x,t) \]
であるから、
\[ \frac{\partial \psi_k(x,t)}{\partial t} = -i\frac{\hbar k^2}{2m}\psi_k(x,t) \]
を得る。
\[ \frac{\partial \ln \psi_k(x,t)}{\partial t} = \frac{1}{\psi_k(x,t)}\frac{\partial \psi_k(x,t)}{\partial t} \]
であるから、時間について積分すれば
\[ \ln \psi_k(x,t) = -i\frac{\hbar k^2}{2m}t+C \]
\(\small t=0\)のとき境界条件を満たすように積分定数\(\small C\)を定めれば
\[ \psi_k(x,t) = \exp\left(ikx-i\frac{\hbar k^2}{2m}t \right) \]
を得る。したがって、\(\small \psi(x,t)\)は
\[ \begin{align*} \psi(x,t) &= \int_{-\infty}^\infty A_k\psi_k(x,t) dk \\ &= \int_{-\infty}^\infty A_k\exp\left(ikx-i\frac{\hbar k^2}{2m}t \right) dk \end{align*} \]
と計算できる。
境界条件からフーリエの定理(逆フーリエ変換)を用いて、確率振幅\(\small A_k\)を求めると、
\[ A_k = \frac{1}{2\pi}\int_{-\infty}^\infty \psi(x,0)\exp(-ikx)dx \]
であるから、
\[ A_k = \frac{1}{2\pi} \frac{1}{\sigma^{1/2}\pi^{1/4}}\int_{-\infty}^\infty \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right)\exp(-ikx)dx \]
となる。積分の中身を\(\small x\)について平方完成すると
\[ \begin{align*} &\exp\left(-\frac{x^2}{2\sigma^2}+i\left(\frac{\bar{p}}{\hbar}-k\right)x \right) \\ &=\exp\left(-\frac{\left(x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right)\right)^2}{2\sigma^2} \right) \exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right) \end{align*} \]
を得る。
\[ \begin{align*} &A_k = \frac{1}{2\pi} \frac{1}{\sigma^{1/2}\pi^{1/4}}\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right) \\ &\qquad\quad\int_{-\infty}^\infty \exp\left(-\frac{\left(x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right)\right)^2}{2\sigma^2} \right) dx \end{align*} \]
であるが、積分は
\[ \begin{align*} &\small \int_{-\infty}^\infty \exp\left(-\frac{\left(x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right)\right)^2}{2\sigma^2} \right) dx = \int_{-\infty}^\infty \exp\left(-\frac{z^2}{2\sigma^2} \right) dz = \sqrt{2\pi\sigma^2} \\ &z = x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right) \end{align*} \]
と計算できる。\(\small z\)は複素数であるが、実数と同じように最後の等式が成り立つらしい(正規分布の式を思い出せば理解できるだろう)。したがって、
\[ A_k = \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}}\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right) \]
が成り立つ。
あとは、この\(\small A_k\)を\(\small \psi(x,t)\)の式に代入して積分を計算すればよい。
\[ \psi(x,t) = \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}}\int_{-\infty}^\infty \exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2+ikx-i\frac{\hbar k^2}{2m}t \right) dk \]
であるから、\(\small k\)について平方完成して積分を計算する。非常に複雑であるが
\[ \begin{align*} &\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2+ikx-i\frac{\hbar k^2}{2m}t \right) \\ &=\exp \left(-\frac{1}{2}\left(\sigma^2+\frac{i\hbar t}{m} \right)\left(k-\frac{\sigma^2\bar{p}/\hbar+ix}{\sigma^2+\frac{i\hbar t}{m}} \right)^2 \right) \\ &\quad\times \exp \left(-\frac{1}{2\left(\sigma^2+\frac{i\hbar t}{m} \right)}\left(x^2-2i\sigma^2\bar{p}/\hbar\left(x-\frac{\bar{p}}{2m}t\right) \right) \right) \end{align*} \]
となる。積分がかかるのは平方完成した部分のみであるから、正規分布の計算を思い出せば
\[ \begin{align*} &\int_{-\infty}^\infty \exp \left(-\frac{1}{2}\left(\sigma^2+\frac{i\hbar t}{m} \right)\left(k-\frac{\sigma^2\bar{p}/\hbar+ix}{\sigma^2+\frac{i\hbar t}{m}} \right)^2 \right) dk \\ &= \sqrt{2\pi}\frac{1}{\sigma\sqrt{1+\frac{i\hbar t}{m\sigma^2}}} \end{align*} \]
が成り立つことが分かる。したがって
\[ \begin{align*} \psi(x,t) & = \frac{1}{\sigma^{1/2}\pi^{1/4}}\frac{1}{\sqrt{1+\frac{i\hbar t}{m\sigma^2}}} \\ & \times \exp \left(-\frac{1}{2\left(\sigma^2+\frac{i\hbar t}{m} \right)}\left(x^2-2i\sigma^2\bar{p}/\hbar\left(x-\frac{\bar{p}}{2m}t\right) \right) \right) \end{align*} \]
と計算できる。\(\exp \)の中身が理解しづらいので、分子と分母に\(\small (\sigma^2-i\hbar t/m) \)を掛けて式を整理する。分母は
\[ 2\left(\sigma^2+\frac{i\hbar t}{m} \right)\left(\sigma^2-\frac{i\hbar t}{m} \right)=2\sigma^4\left(1+\left(\frac{\hbar t}{m\sigma^2}\right)^2\right) \]
となる。分子は実数の項と虚数の項を分けて計算する。分子を
\[ \varphi =-\left(x^2-2i\sigma^2\bar{p}/\hbar\left(x-\frac{\bar{p}}{2m}t\right) \right)\left(\sigma^2-\frac{i\hbar t}{m}\right) \]
と置けば、実数部分は
\[ \Re[\varphi]=-\sigma^2\left(x^2-2\frac{\bar{p}}{m}t\left(x-\frac{\bar{p}}{2m}t \right) \right)=-\sigma^2\left(x-\frac{\bar{p}}{m}t \right)^2 \]
となり、虚数部分は
\[ \Im[\varphi] = i\left(\frac{\hbar t}{m} x^2+2\sigma^4\frac{\bar{p}}{\hbar}\left(x-\frac{\bar{p}}{2m}t \right) \right) \]
となる。この式はうまく整理すると
\[ \Im[\varphi] =i\left(\frac{\hbar t}{m}\left( x-\frac{\bar{p}}{m}t\right)^2+ 2\sigma^4\left(1+\left(\frac{\hbar t}{m\sigma^2}\right)^2\right)\frac{\bar{p}}{\hbar}\left(x-\frac{\bar{p}}{2m}t \right) \right) \]
と計算できる。したがって、最終的な解は前節で示した通り
\[ \begin{align*} \psi(x,t) \; & = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left( x -\frac{\bar{p}}{m}t \right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{\hbar}x -\frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left( x -\frac{\bar{p}}{m}t \right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right) \end{align*} \]
と得ることができる。
光子の場合
自由状態の電子の座標に関する確率分布を計算したが、同様の方法で光子の座標に関する確率分布を求めてみよう。光子の場合、電磁気学の知識がある読者であれば基礎方程式はマックスウェル-ヘルツの方程式(電磁波の基礎方程式)
\[ \frac{1}{c^2}\frac{\partial^2 \psi(x,y,z,t)}{\partial t^2}=\frac{\partial^2 \psi(x,y,z,t)}{\partial x^2}+\frac{\partial^2 \psi(x,y,z,t)}{\partial y^2}+\frac{\partial^2 \psi(x,y,z,t)}{\partial z^2} \]
であると思われるかもしれない。しかし、実を言うと相対論的な量子力学ではこの基礎方程式は光子の波動関数の時間発展を記述する方程式としてはうまく機能しないことが知られている。厳密には、ディラック行列といわれる
\[ \gamma_i^2=1, \gamma_i\gamma_j=0, \quad i,j = 1,2,3 \]
を満たす係数を用いて、1次の偏微分方程式に置き換えた
\[ \frac{1}{c}\frac{\partial \psi(x,y,z,t)}{\partial t}=\gamma_1\frac{\partial \psi(x,y,z,t)}{\partial x}+\gamma_2\frac{\partial \psi(x,y,z,t)}{\partial y}+\gamma_3\frac{\partial \psi(x,y,z,t)}{\partial z} \]
が基礎方程式である。両辺を2乗すれば、ディラック行列を消去することができて
\[ \small \frac{1}{c^2}\left(\frac{\partial \psi(x,y,z,t)}{\partial t}\right)^2=\left(\frac{\partial \psi(x,y,z,t)}{\partial x}\right)^2+\left(\frac{\partial \psi(x,y,z,t)}{\partial y}\right)^2+\left(\frac{\partial \psi(x,y,z,t)}{\partial z}\right)^2 \]
と表すことができる。
もちろん、3次元の場合は計算が難しいので、空間が1次元の場合の光子の座標に関する確率分布を求めよう。シュレディンガー方程式同様に
\[ \begin{align*} &\frac{1}{c^2}\frac{\partial \psi(x,t)}{\partial t}\frac{\partial \psi^{\ast}(x,t)}{\partial t}=\frac{\partial \psi(x,t)}{\partial x}\frac{\partial \psi^{\ast}(x,t)}{\partial x} \\ &\psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right) \end{align*} \]
であるときの\(\small \psi(x,t)\)を求めればよい。\(\small \psi(x,t)\)は複素関数であるから二乗は複素共役を掛けて計算することに注意する。光子のエネルギーを
\[ E^2 = p^2c^2 \; \Rightarrow \; EE^\ast=(pc)(pc)^\ast \]
とすれば、一応対応原理から導出できる基礎方程式になっている。
境界条件をフーリエ変換して
\[ \psi(x,0) = \int_{-\infty}^\infty A_k\exp(ikx) dk \]
と置く。
\[ \frac{\partial \psi_k(x,t)}{\partial x} = ik\psi_k(x,t) \]
を仮定して、基礎方程式に代入すれば
\[ \frac{\partial \psi_k(x,t)}{\partial t} = \pm ick\psi_k(x,t) \]
を得る。符号が2つあるので、この符号は確率\(\small 1/2\)ずつでランダムに決定されると仮定しよう。この場合、時間について積分して、\(\small t=0 \)のとき境界条件を満たすように積分定数\(\small C \)を定めれば
\[ \psi_k(x,t) = \frac{1-i}{2}\exp\left(ik(x-ct) \right)+\frac{1+i}{2}\exp\left(ik(x+ct) \right) \]
と置けば、\(\small \psi_k(x,0)=\exp(ikx)\)となるだろう。係数は複素共役を掛けた際に、交差項が相殺され、かつ、それぞれの項が\(\small 1/2\)になるように定めている。境界条件のフーリエ変換は前節同様に
\[ A_k = \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}}\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right) \]
である。
あとは
\[ \psi(x,t) = \int_{-\infty}^\infty A_k\psi_k(x,t) dk \]
を計算すればよい。\(\small k \)について平方完成すると
\[ \begin{align*} &\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2+ik(x\pm ct) \right) \\ &=\exp \left(-\frac{\sigma^2}{2}\left(k-\frac{\sigma^2\bar{p}/\hbar+i(x\pm ct)}{\sigma^2} \right)^2 \right) \\ &\quad\times \exp \left(-\frac{1}{2\sigma^2}\left(\left(x\pm ct \right)^2-2i\sigma^2\bar{p}/\hbar\left(x\pm ct\right) \right) \right) \end{align*} \]
となる。積分がかかるのは平方完成した部分のみであるから、正規分布の計算を思い出せば
\[ \int_{-\infty}^\infty \exp \left(-\frac{\sigma^2}{2}\left(k-\frac{\sigma^2\bar{p}/\hbar+i(x\pm ct)}{\sigma^2} \right)^2 \right) dk = \frac{\sqrt{2\pi}}{\sigma} \]
が成り立つことが分かる。したがって
\[ \begin{align*} \psi(x,t)= \frac{1}{\sigma^{1/2}\pi^{1/4}} & \Biggl[ \frac{1-i}{2} \exp \left(-\frac{\left(x- ct \right)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}(x-ct) \right) \\ &+\frac{1+i}{2}\exp \left(-\frac{\left(x+ct \right)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}(x+ct) \right) \Biggr] \end{align*} \]
と計算できる。確率分布を計算すると
\[ P(x,t) = |\psi(x,t)|^2 = \frac{1}{2}\frac{1}{\sqrt{\pi\sigma^2}}\left[\exp \left(-\frac{\left(x- ct \right)^2}{\sigma^2} \right)+\exp \left(-\frac{\left(x+ ct \right)^2}{\sigma^2} \right) \right] \]
を得る。光子の速度が光速\(\small c\)で一定でなければならないことを考えれば、この確率分布は直感的に妥当なものであることが理解できるだろう。ただし、光子はエネルギーなど観測できる物理量に離散性があることが知られており、厳密には観測できる\(\small (x,t) \)について何らかの制約(離散性)があるかもしれないことに注意する必要がある。また、ここにおける時間\(\small t \)というものは我々が認識している時間とは異なるものであるため、意味のある計算結果ではないかもしれない。
量子の運動はブラウン運動ではない
前節までで本稿の内容は終わりであるが、筆者が書いた本の宣伝もかねて、小話を書いて締めくくろう。実をいうと、量子の運動を確率過程で記述したいという願望は昔から存在している。シュレディンガー自身もマックス・ボルンが提唱した波動関数の確率解釈という説に拒絶反応を示したらしく、これを否定するために考えたのがシュレディンガーの猫という思考実験であるということだった。もし、波動関数の確率解釈が正しいと考えるならば、確率的な運動方程式(すなわち、確率過程)で量子の運動が記述できなければおかしいという考え方をシュレディンガーは持っていたようである。
この確率的な運動方程式で量子の運動を記述しようという考え方はファインマンに継承されて、彼が構築した理論が経路積分という理論体系になっている。ただし、経路積分は数学者から強い批判を受けており、数学的に定義できない(計算できない)はずの積分を計算結果が合うように適当に計算してしまっているという意味で、数学的な基礎を欠いている理論であると言われている。この経路積分の数学的基礎付けという問題は現在においても未解決な問題であるらしい(筆者には真偽は不明であるけど)。
ただ、1940年代に日本の数学者の伊藤清が開発したブラウン運動に関する確率積分、確率微分方程式の理論が急速に発展したということもあり、ブラウン運動の理論で経路積分の数学的な基礎付けができないかということが考えられたようである。ファインマン自身も数学者のMark Kacと共同でブラウン運動の理論を用いて経路積分の理論を構築できないかということを研究していたようである(この研究の過程で考えられたのがFeynman-Kacの公式であるらしい)。現代においても、量子力学の理論をブラウン運動や確率微分方程式で記述しようという研究は後を絶たず、ネットや雑誌などで無数の論文を発見することができる。
しかし、本稿で示した通りシュレディンガー方程式の解が表す確率分布は
\[ x(t) \sim N\left(\frac{\bar{p}}{m}t, \;\frac{\sigma^2}{2} + \frac{\hbar^2}{2m^2\sigma^2}t^2 \right) \]
であり、この確率分布はブラウン運動の確率分布と明らかに異なっている。ブラウン運動であるならば
\[ x(t) \sim N\left(\frac{\bar{p}}{m}t, \; \frac{\hbar}{m}t \right) \]
でなければならないだろう。別の考え方として、シュレディンガー方程式の解で\(\small \bar{p}=0\)とおいて、虚数部分のみをとると
\[ K(x,t) = \exp \left(i \left\{ \frac{\hbar t x ^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right) \]
と表すことができる。分母について、\(\small (\hbar t /m\sigma^2)^2 \gg 1\)と仮定して近似して、定数部分を調整すると
\[ K(x,t) = \frac{1}{\sqrt{2\pi\frac{i\hbar}{m}t}} \exp \left(- \frac{x ^2}{2 \frac{i\hbar}{m}t} \right) \]
と表せる。この式は熱伝導方程式で表すことができて
\[ \frac{\partial K(x,t)}{\partial t} = \frac{i\hbar}{2m} \frac{\partial^2 K(x,t)}{\partial x^2} \]
となる。両辺に\(\small i\hbar\)を掛ければ
\[ i\hbar\frac{\partial K(x,t)}{\partial t} = -\frac{\hbar^2}{2m} \frac{\partial^2 K(x,t)}{\partial x^2} \]
となり、シュレディンガー方程式っぽく見えなくもない。このことから、時間か質量、もしくは、ボラティリティが虚数のブラウン運動を用いて量子の運動を記述できるのではないか、という考え方もあるようである。しかし、これはただの類推であるし、波動関数はそれ自体が確率分布関数であるわけではない。したがって、こういった計算に意味を見出すことはできないと考えられる。
以上の考察から、ブラウン運動で量子力学の理論を構築したい、経路積分に数学的な基礎を提供したいという考えは初歩的なところで間違っていることが理解できるだろう。もしあなたがブラウン運動の理論と量子力学を学び、この2つを紐づけることで量子力学の理論を構築したいという野心をもっているのならば、時間の無駄であるからやめておいた方が良いと指摘しておきたい。まあ、もう何年、何十年と研究してしまっていて引き返すことができない人たちは知らんけど・・・
それでは、量子力学の理論を確率過程論で構築することが不可能であるかというと、それも違うと筆者は考える。ただ、これを構築するためには我々があまりにも無条件に正しいと信じ込んでしまっているある前提を否定しなければならないということであり、なかなか気づくことができないし、気づいたとしても受け入れることが難しい理論になっている。言い換えれば、”量子力学を理解したと思ったならば、それは量子力学を理解していない証拠である”ということを思い知らされるような主張になっている。こういった理論に興味があるという読者の方は筆者の著書を紐解いてみることをお薦めする。長々と文章を書いて自分の本の宣伝をしたかっただけかい、という批判は聞こえないことにしておこう・・・
参考文献
[1] 朝永振一郎 (1997), 量子力学Ⅰ(第2版), みすず書房
[2] 朝永振一郎 (1997), 量子力学Ⅱ(第2版), みすず書房
[3] 平野要 (2022), 多時間理論による量子力学ー二重スリット実験に関する一考察ー, Amazon Kindle Store(英語訳:Hirano, Kaname (2022), Quantum Mechanics with Multi-Time Theory, Amazon Kindle Store.)
[4] 平野要 (2024), 複素関数とシュレディンガー方程式, Amazon Kindle Store(英語訳:Hirano, Kaname (2024), Complex Functions and Schrödinger Equation, Amazon Kindle Store.)
[5] Feynman, Richard. P. and Albert. R. Hibbs (1965), Quantum Mechanics and Path Integrals, McGraw-Hill, Inc.(日本語訳:ファインマン、ヒッブス(2017), 経路積分と量子力学(新版), みすず書房)
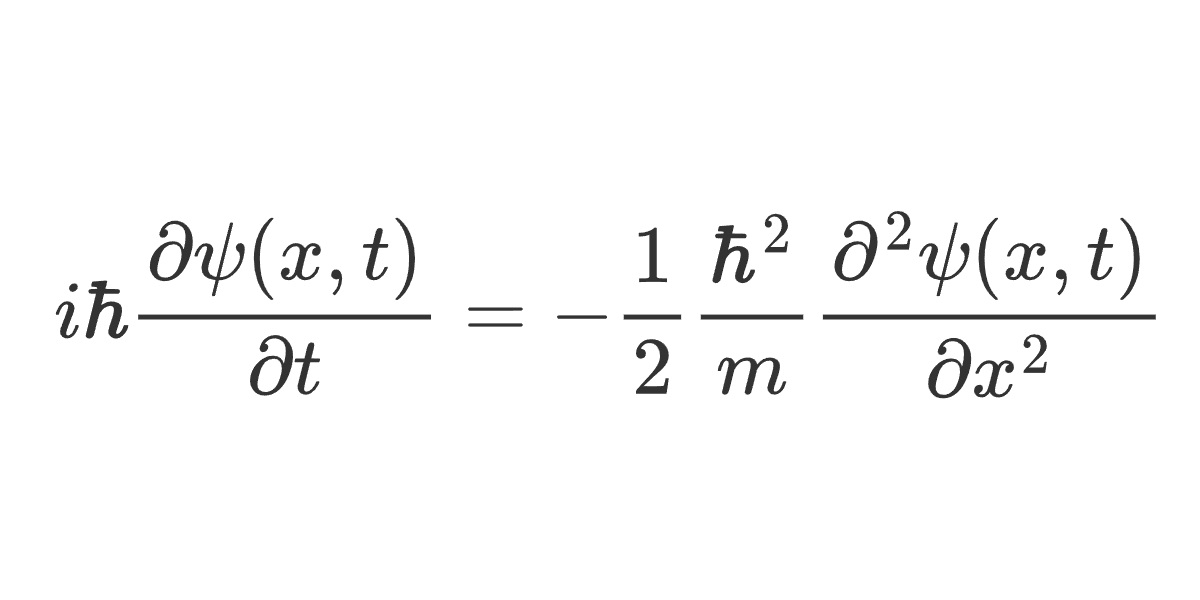


コメント