概要
モバイルゲームの開発に手を付け始めたので、テキサスホールデムのAIのアルゴリズムの考察が遅れ気味であるが、プリフロップは一旦目途がついたということで、今回はフロップにおける行動モデルを考える際の大まかな方針をまとめていこう。
手札と共通カードの抽象化
フロップ以降は手札と共通カードの組み合わせが急増するため、プリフロップのようにカードの組み合わせごとに戦略を考えることは現実的ではない。そのため、手札と共通カードから推測できるエクイティ(近似的には、勝利確率)を計算して、そのエクイティ毎に採用する戦略を変更するモデルを考える。より精緻にするには対戦相手のハンドレンジを推測(プレイ履歴からベイズ推定したり、GTO戦略を仮定する)して、そのハンドレンジに基づいたエクイティを計算するべきであるが、筆者が考えているゲームはプレイヤーに勝たせることを想定しているゲームであるため、それほど強いNPCである必要性はないだろう。そのため、簡易的にAny Handを前提としてエクイティを計算すればよいだろう(試してみて不合理に見える場合は、なんちゃってGTOみたいなのを仮定して計算する方法を検討する)。
プレイヤーの選好の反映
プレイヤーの不合理な選好を行動に反映するためには、上記で計算したエクイティにバイアスを掛けることで表現する。このバイアスは、以下の要因に影響されると推測される。
- 手札:ポケットペアやA,Kを持っている場合ハイカードでも強気になるなど
- 手札と共通カードでできる役:フラッシュやフラッシュドローで強気になる、ストレートやストレートドローで強気になる、トップペアで慎重すぎるなど
1.はプリフロップのモデルパラメータを継承して利用すればよいだろう。2.はプリフロップのモデルパラメータを継承する部分とフロップ固有のパラメータ(役やフラッシュドロー、ストレートドロー、バックドアなどでバイアスを掛ける)を導入した方が良いかもしれない。
エクイティの確率分布
フロップにおけるプレイヤーの行動モデルを考える際にエクイティを評価基準にすると書いたが、実際には対戦相手が持つ手札の強さとの競争であるから、たとえ自分の手札が上位10%の手札の強さであっても、対戦相手がそれ以上に強い手札を持っていれば負ける確率が高いということになる。すなわち、エクイティの絶対水準よりも、エクイティの相対的な順位の方が手札の強さを表す基準として重要になる。やっかいな問題であるが、エクイティの確率分布は一様分布ではない。言い換えれば、例えばエクイティ(勝利確率)が90%という場合、上位から10%の順位にある手札という意味ではないということになる。
具体的に、フロップにおけるエクイティの確率分布をプレイヤー数毎に計算すると以下のような確率分布になっている。これはシミュレーションで手札とフロップにおける共通カードの状態を生成し、そこからさらにシミュレーションをして勝利確率を計算するという方法で推定している(Simulation in Simulation)。計算時間が非常にかかる手法であり、10000回×10000回で1億回近いシミュレーション計算をしており、半日近くPCで計算する羽目になった。
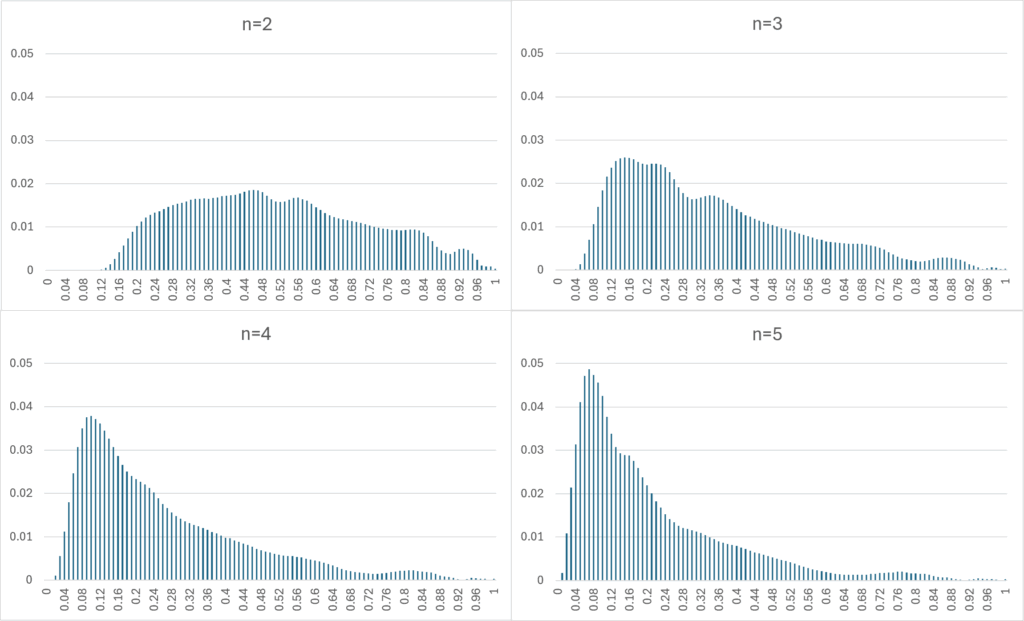
例えば、プレイヤーが2人の場合にエクイティ(勝利確率)が90%と言う場合は、上位3%ぐらいの範囲に入っており、見かけの勝利確率より手札としては強い印象になるかもしれない。これは人数が増えるほど低くなる傾向があり、プレイヤーが5人の場合はエクイティが67%程度でも上位3%ぐらいになる。この場合、
- プレイヤーが2人の場合にエクイティが90%
- プレイヤーが5人の場合にエクイティが67%
の二つの状況は同程度に強気になる状況であると考えなければならないだろう。フロップにおける戦略を考える場合は、これを適切に換算して考える必要がある。
エクイティをスコアに換算する方法
ある状況において、自分のエクイティが\(\small p\)と推定できるものとする。エクイティの確率密度関数を\(\small \phi(p)\)、確率分布関数を\(\small \Phi(p)\)と表す。このとき
\[ \small \Phi(p) = \int_0^p\phi(z)dz \]
である。\(\small \phi(p)\)は前節で図示した確率分布関数を表す。エクイティを持っている手札の強さに換算するために\(\small s = \Phi(p)\)をスコアということにする。ランダムの手札と共通カードの組み合わせからスコア\(\small s\)が従う確率分布を計算すると一様分布\(\small U[0, 1]\)になることを理解できることだろう。この一様分布に従う数値に基づいて、NPCの行動を決定することで、様々な状況における行動の基準を統一的に扱うことができる。
テキサスホールデムでは、人数やベッティングラウンド(Flop, Turn, River)で手札の役が出来る確率や完成した役が相対的にどれぐらいの強さを持っているかが変わってしまうのであるが、上記の方法で一様分布に従うスコアに変換して、そのスコアを基準に行動(レイズ、コール、フォールド)を決定することである程度共通化した行動モデルを作ることができるだろう。
その他の状態
手札と共通カード以外に行動を変える要素として以下のような情報を状態として扱う必要がある。
- アグレッサーかどうか(ドンクベットされた場合はアグレッサーでないものとして意思決定)
- ポジション(IPかOOPか)
- 残存プレイヤーの数
- ポットとスタックの比率(SPR: Stack Pot Ratio)
これらの情報をどのように扱うかはフロップにおけるプレイヤーの行動モデルの詳細な仕様を検討する際に考察しよう。
行動の選択肢の簡略化
ベットやレイズのチップ量はミニマムレイズの額を上回っていれば任意の数量を指定することができる。しかし、現実に連続的な数値の意思決定を扱うことは数学的に容易ではないため、意思決定で選べる選択肢を離散化した方が良いだろう。実際のゲームでも任意の数量を指定できるようにしても、操作しづらいだけであるため、ゲームのUIで選択肢を絞る方が現実的だろう。具体的には、以下のような数値を選べればよいかもしれない。
ベット:ポットの0(Check), 1/12, 1/6, 1/4, 1/3. 1/2, 2/3, 3/4, 1, 1.5, 2, 3, all-in
レイズ:ベットの0(Fold), 1(Call), 2, 2.5, 3, 3.5, 4, 5, 6, 9, 12, 16, all -in
いずれも倍率を表す数値であることに注意する。レイズは一度で2回レイズを重ねた分ぐらいの倍率が指定できれば十分だろう。スタックが100bbの場合は、ベットが3bbであればオールインで33倍であるから大きな抜けは生じないように見える。
ターン、リバーへの拡張、その他の拡張
フロップにおけるプレイヤーの行動モデルということで考察してきたが、ターンやリバーにおけるエクイティをスコアに換算する際の確率分布が異なるだけであり、基本的には同じアプローチを採用することができる。あとはターンやリバーにおける意思決定の癖(ターンで慎重になる、リバーでブラフを使う比率が上がる、など)みたいなのをパラメータとして定義してあげれば、プレイヤーの行動モデルを一通り定義できるだろう。次回以降では次のような順番でフロップ、ターン、リバーにおけるプレイヤーの行動モデルを深堀していこうと思う。
- フロップにおける行動モデルの詳細化
- ターン、リバーにおける行動モデルの詳細化
- 実装してみて、精緻化が必要な個所があれば修正
- プロトタイプの実装
また、本稿のアプローチはエクイティを基準にしているため、テキサスホールデム以外のゲームにもある程度近い形で応用することができる。ショートデッキホールデムやオマハホールデムへの応用も可能ということで、人間らしいプレイがある程度再現できれば、ルールを変えたゲームにも応用できる行動モデルになることが期待できる。


