最適プリフロップオールイン
1回変な投稿をはさんだ気がするが、前回に引き続いて反実仮想リグレット最小化の応用を考えよう。プレイヤーが二人しかいないテキサスホールデム(ヘッズアップ)を考える。プレイヤーが二人の場合は、ナッシュ均衡戦略が一意に定まるため(2人が採用する戦略を対称にできるため)、GTO戦略をどれだけ極めているかの勝負であり、実力差が最も顕著に現れるゲームの形態であると思うかもしれない。実際に、ヘッズアップの勝負を相手に申し込むということは、”どうせお前俺より下手なんだろ?”と言っているようなものであり、喧嘩を売っていると捉えられることもあるようである。
しかし、現実には実力差があって勝てないと思う場合でも、工夫をすることでヘッズアップはただの運ゲーに変えることができる。すなわち、プリフロップからオールインするか、フォールドするかの二択にしてしまえば、対戦相手もオールイン(コール)するか、フォールドするかを選択するしかなくなるということである。言い換えれば、最適なプリフロップオールインの手札の選択さえ適切に行えば、ヘッズアップは互角の戦いに持ち込むことができるということになる(もちろん、お互いが最適な戦略を採用している場合は勝ち越すことはできないけど)。スタックが深い状態では対戦相手がオールインに応じるつもりがないとフォールドばかりになってしまうため、利用することが難しい部分があるが、50bb以下ぐらいのスタックであればプリフロップオールインで決着をつけることは現実的な戦略の一つであるかもしれない(こういった戦略はPush or Foldといわれる)。前回説明したCounterfactual Regret Minimalizationを用いて、最適なヘッズアップオールイン戦略を求めてみようというのが本稿の内容である。
2人のプレイヤーがオールインかフォールドしか選択しないと仮定した場合、SBとBBの選択肢と結果に対する利得表は次の通りである。
| SB | BB | |
|---|---|---|
| SBがフォールド | -0.5bb – Ante | 0.5bb + Ante |
| SBオールイン、BBフォールド | 1bb + Ante | -1bb – Ante |
| SB,BBオールイン、SB勝利 | +Stack | -Stack |
| SB,BBオールイン、BB勝利 | -Stack | +Stack |
| SB,BBオールイン、チョップ | 0 | 0 |
この問題を考える際に影響があるファクターとしてスタックのサイズが挙げられる。SBとBBで支払うブラインドが異なるため、これが原因でSBとBBで採用すべきハンドレンジが異なることになる。スタックが大きいほど、オールイン時の損益と比較してフォールド時の損益が相対的に小さくなるため、オールインのレンジが狭くなる傾向があると推測できるだろう。そのため、いくつかのスタックについて具体的なハンドレンジを求めてみよう。
具体的な計算アルゴリズムは以下の通りである。SBとBBで最適な戦略が異なるため、反実仮想リグレットはポジションごとに計算する必要があることに注意する。
- 2人のプレイヤーの2枚の手札\(\small h_{SB},h_{BB}\)をランダムにドローする。ここで、\(\small h_{SB},h_{BB}\)は169通りのハンドを表すものとする(1326通りのカードの組み合わせで計算する必要はない)。
- 戦略関数のテーブル\(\small \pi_{\text{SB}}[h_{SB}]\)に従って、SBのアクション(オールイン or フォールド)を決定する。フォールドの場合は利得を確定し、5.に進む。
- SBの選択がオールインの場合、戦略関数のテーブル\(\small \pi_{\text{BB}}[h_{BB}]\)に従って、BBのアクション(オールイン or フォールド)を決定する。
- 共通カード5枚をランダムにドローし、プレイヤーの勝敗を決定する。決定された2人のプレイヤーの役とアクションから利得\(\small r_{\text{mixed},k},k \in\{\text{SB},\text{BB}\}\)を計算する。
- 各プレイヤーのリグレットを以下の式で計算し、集計値に加算する(ポジションごとに区別して集計する。)。
\[ \small \begin{align*} &R_{\text{all-in},k}(h) = \frac{1}{T} \sum_{t=1}^Tr_{\text{all-in},k}(h, t)-r_{\text{mixed},k}(h, t) \\ &R_{\text{fold},k}(h) = \frac{1}{T} \sum_{t=1}^Tr_{\text{fold},k}(h, t)-r_{\text{mixed},k}(h, t), \;k \in\{\text{SB},\text{BB}\} \end{align*} \]
\(\small r_{\text{all-in},k},r_{\text{fold},k}\)は戦略関数が出した決定にかからわず、オールインを選択した場合、フォールドを選択した場合の利得である。戦略関数と一致する行動では0であるが、戦略関数と異なる行動では異なる利得が生じる。集計されたリグレットから手札に対応するオールインとフォールドの選択確率を更新する。 - 1.から5.までの手続きをシミュレーション回数分繰り返し、最適な戦略関数を決定する。
実際に開発したツールのリンクは以下である。
レーキの設定ができたり、目的関数としてべき乗関数
\[ \small U(s) = s^{1-\gamma} \]
の\(\small \gamma\)の値を指定できるように拡張してある。シミュレーションの収束性は非常に悪く、最低でも100万回、可能であれば1000万回ぐらいは計算が必要である。1000万回だと5~10分計算に時間がかかるので、計算する場合はしばらくPCが占有されてもいい場合に行うといいだろう。といいつつも、自分で計算する奇特な読者などきっといないと思うので、あらかじめ計算した結果が見れるページも用意しておいた。
トーナメントで利用する場合が多いと思われるため、スタックが2~20bbぐらいまでを細かく計算した。アンティが0.125bb,0.25bbの場合も計算しておいた。必要に応じて参照すればよいだろう。具体的に計算した結果を確認してみよう。
結果
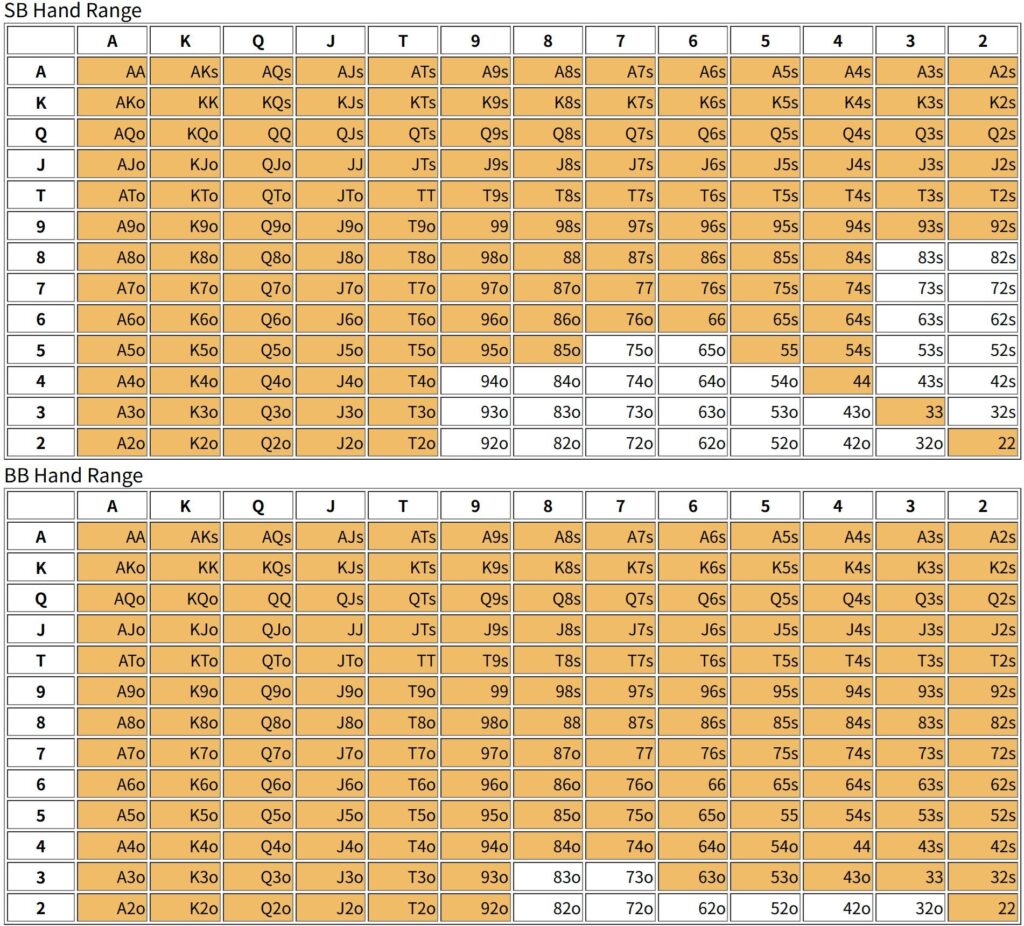
いくつかの条件について考察しよう。具体的にスタックが3bb,5bb,10bb,50bbの場合のハンドレンジを示すと次の通りである。
[3bb]
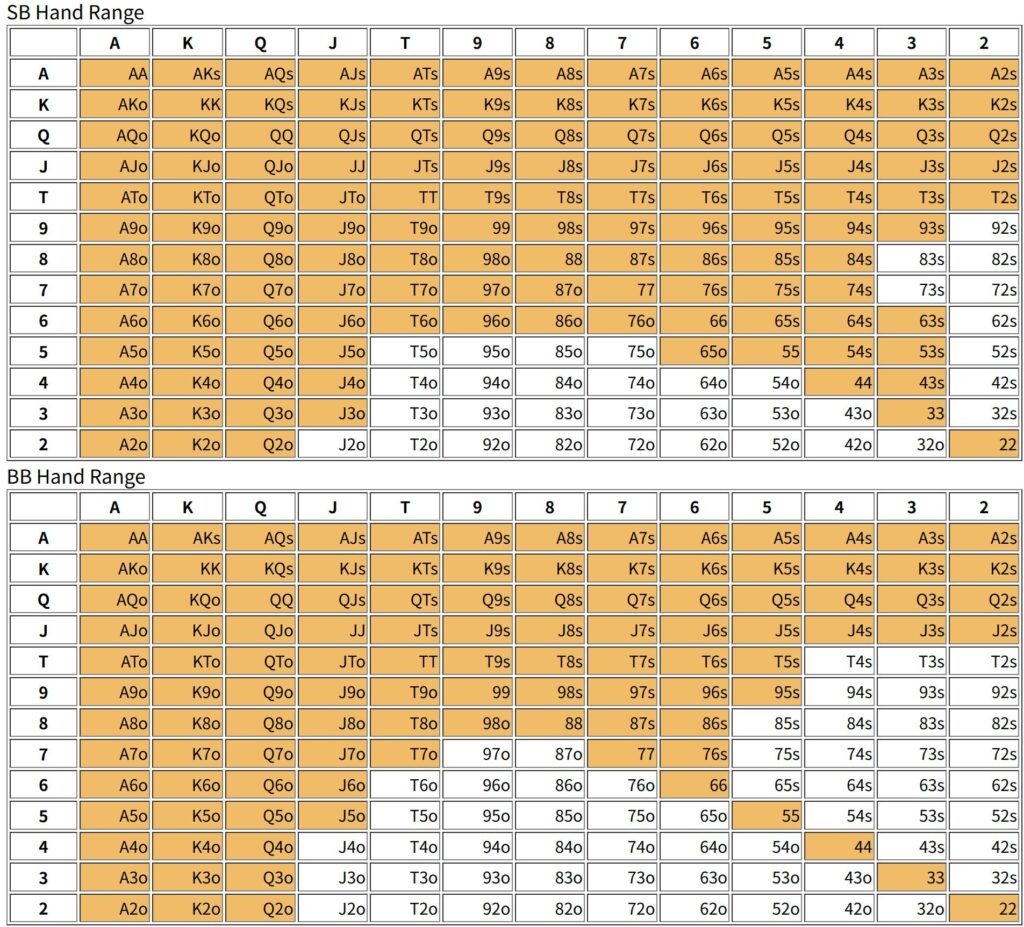
[5bb]
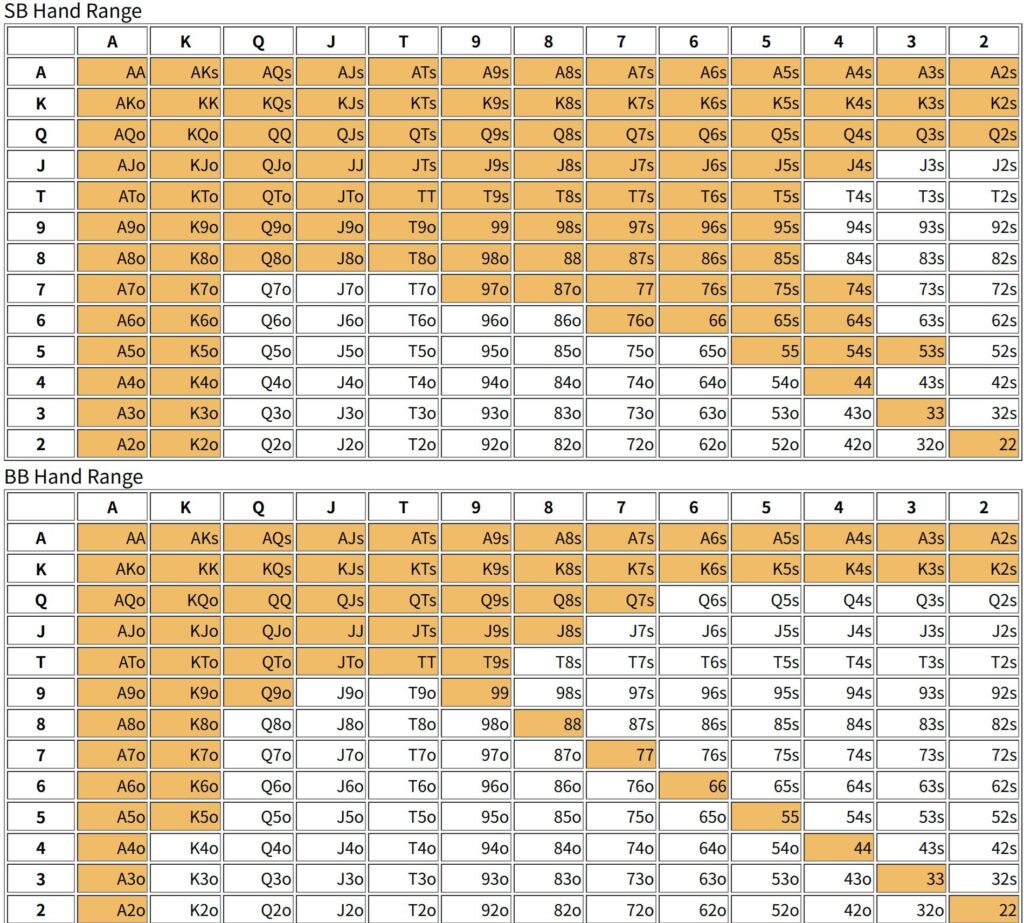
[10bb]
[50bb]
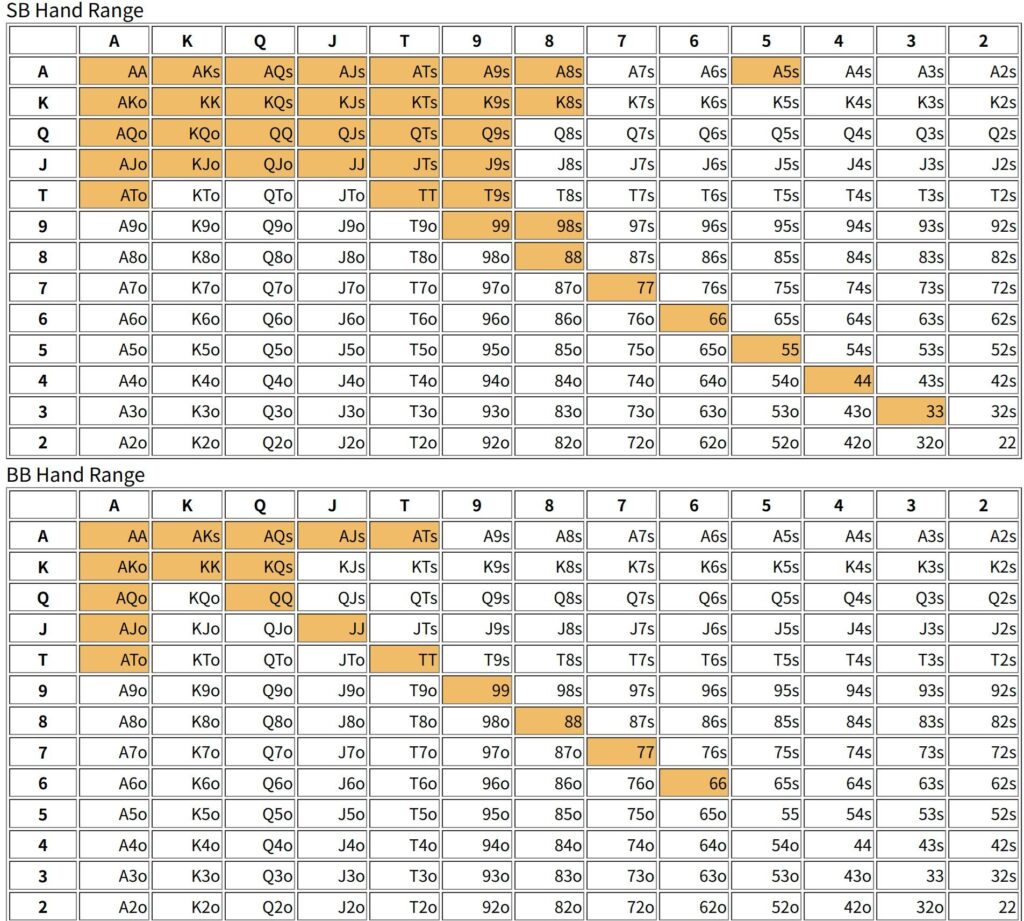
不思議に感じるかもしれないが、一般的にはSBのハンドレンジの方が広い。おそらく、BBがフォールドする可能性があるため、ブラフの要素が含まれるのだろう。しかし、本来はブラインドの負担はBBの方が重いため、BBの方がハンドレンジは広いはずだろう。これはスタックが少なくなると観察できる傾向で大体スタックが5bb辺りでハンドレンジの広さが逆転する。
もう一つ重要な傾向として、SBのハンドレンジの方がSuitedやConnectedを多く含むレンジが選ばれることである。スタックが相応にあると、SBはブラフを含むため投機的なハンドをいくばくか含む必要があるということだろう。BBはポケットペアやAx、Kxに偏ったハンドレンジを選ぶ傾向があるようである。後攻であるため、ディフェンスに向いた手札を選ぶことになる。このように考えると、ハンドレンジはプレイヤーの選好以外にポジションによっても変化するということになるかもしれない。この辺りはまた今後検討することにしよう。
結論と今後の拡張
Further Extensionなんかあるのかという話であるが、プレイヤーが3人以上についても拡張を考えたい。この場合、手前のプレイヤーがオールインするかフォールドするかでハンドレンジが変わることになる。例えば、4人プレイの場合は、BTNはCOがオールインするかフォールドするかで異なるし、SBは4通りの組み合わせについて戦略を考えなければならない。また、3人以上のプレイではナッシュ均衡が無数に存在するため、最適な戦略は対戦相手のハンドレンジに依存して変化するということになるだろう。ただし、CFRで計算したハンドレンジというのも計算できるし、比較的バランスの良いレンジ構築になるであろうことが予想できるため、これも時間がかかるかもしれないが計算してみよう。
もう一つは、AIを相手にテキサスホールデムの対戦ができるゲームを筆者は考えているが、オールインとフォールドに選択肢を絞ったゲームも相応に面白いかもしれない。最適な選択の推奨を見ながら実際のゲームでプレイしてみることで、様々な状況でオールインするべき手札かどうかを確かめてみることもできるかもしれない。これもそのうち実装してみようと思う。



