※このページは筆者が過去に書いたペーパー”A Quantum Mechanical Financial Time Series Model”の日本語訳である。注意点として、本稿ではSchrödinger方程式から等価な確率過程を導いているが、実をいうとこの計算は間違っている。ただし、非常にうまい間違い方をしており、後に正しい計算方法に気づくきっかけになったペーパーである。正しい計算方法について知りたい場合は、『多時間理論による量子力学』を参照いただきたい。
Abstract
本稿では、Schrödinger方程式をリバースエンジニアリングすることによって導出される時系列モデルを紹介する。モデルは確率的なドリフトを三角関数の合成として持つ波束モデルである。このモデルは市場のタイミング戦略によって利益を得る機会を許容する実測度のモデルとそれを許容しない効率的市場仮説のモデルを包含する金融時系列モデルと考えることができる。
概要
金融商品のプライシングとリスク管理に使用される時系列モデルや確率過程は、一般に取引のタイミングを図ることで利益を得ることはできないという前提に基づいている。端的に言えば、効率的市場仮説であるが、タイミング戦略を用いて利益を得ることを目的とする場合、このような時系列モデルは使用することはできない。このようなモデルを構築する場合は、効率的市場仮説とは異なる金融時系列モデルを構築する必要がある。
もちろん、効率的市場仮説が常に間違っており、タイミング戦略でどのような状況でも利益を上げることができると考えるのは適切ではないだろう。 しかし、それを仕事とする人々(例えば、タイミング戦略を方針とするヘッジファンドなど)にとっては、それが常に正しく、いかなる状況においても市場タイミング戦略によって利益を上げることは不可能であるということは受け入れがたいものであるかもしれない。効率的市場仮説は、市場参加者がランダムに振る舞う場合(自由状態)に当てはまるかもしれないが、何らかの外力(ポテンシャル)が働く場合、トレンドが生じたり、周期的な波のように振る舞うと考えることができる。
これと似た現象を扱う分野は量子力学である。自由状態の量子はランダムな確率分布(正規分布)に従うが、ポテンシャルがある状況(束縛状態)では、波のように振る舞い、規則性を持つ。このような挙動は、Schrödinger方程式で表現される。すなわち、Schrödinger方程式から導出された時系列モデルを使用することで、上記の事象を表現し、市場において働くポテンシャルのような何かを表現することができるかもしれない。
しかし、標準的な量子力学では量子の運動は時系列モデルや確率過程では表現されない。これは観測値が時間に関して連続性を持たなかったり、定常状態といわれる時間の経過で性質が変化しない状態を重視しているためと考えられる。主な例外は、Feynmanの経路積分 (Feynman (1965))とNelsonの確率力学(Nelson (1985))である。前者はガウス型のホワイトノイズ過程(状態空間モデル)としてモデル化する方法であり、後者はガウス型ホワイトノイズと同等の分散を持つ平均回帰ドリフトを持つブラウン運動に関連付ける方法である。金融工学の観点からは、後者の方が馴染みやすいが、自由状態における量子の確率分布を考えると前者の方がより自然であるため、本稿では前者のアプローチを採用する。
最終的に提案したい時系列モデルは以下のとおりである。\( \small x(t) \)を時系列データとすれば、
\[ \begin{align*} & \small \bar{x}(t) = \bar{x}(t-1) + \mu + \sum_{j=1}^n \alpha_j \cos \left(2\pi t f_j \right) + \sum_{j=1}^n \beta_j \sin \left(2\pi t f_j \right) \\ & \small x(t) = \bar{x}(t) + \epsilon_t, \quad \epsilon_t \sim N(0, \sigma^2) \\ & \small \mu \sim P(\mu), \quad \alpha_j \sim P(\alpha_j), \quad \beta_j \sim P(\beta_j) \end{align*} \]
である。ここで、\(\small \mu, \alpha_j, \beta_j\)は確率変数、もしくは、確率過程であり、\(\small f_j\)は周波数、\(\small \epsilon_t\) はこのモデルを状態空間モデルと考えた場合の観測ノイズを表す。\(\small \mu, \alpha_j, \beta_j\)が同じ分散の正規分布に従い、\(\small f_j = \frac{j}{2n}\)であるならば、\(\small x(t)\)は正規分布に従い、効率的市場仮説を満たす。しかし、 \(\small \mu, \alpha_j, \beta_j\)が他の確率分布に従ったり、偏った周波数を持つ場合はモデルが生成する軌跡は予測可能であるかもしれない。本稿では、このモデルが量子力学のモデルからどのように導出されるかを順を追って説明する。
Schrödinger方程式と状態空間モデル
最初に Schrödinger方程式から時系列モデルを導出する。これは1個の量子の観測確率分布を無数のアンサンブル(仮想的な粒子)の運動で記述するアプローチであり、そのアンサンブルが従う時系列モデルを求めることに相当する。物理学や量子力学になじみがない読者は、このアンサンブルのドリフト(運動量)と観測ノイズがそれぞれ分散\(\small \sigma_p^2 = \hbar^2/2\sigma^2\)、\( \small \sigma_x^2 = \sigma^2/2\)のホワイトノイズに従っている時系列モデルと考えれば容易に理解できるだろう。これはHeisenbergの不確定性原理\( \small \sigma_p \sigma_x \geq \hbar/2 \)を満たしている。
議論を単純化するため、2次元空間上で\( \small x \)軸方向に直進する正規分布に従う自由状態(すなわち、ポテンシャル0)の量子を考える。初期状態の観測位置と運動量に対応する波動関数は以下で与えられる(古典的な量子力学の教科書を参照(例えば Tomonaga (1962, 1966)))。
\[ \small \psi(x,y,0) = \frac{1}{\sigma\sqrt{\pi}} \exp\left(-\frac{x^2+y^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right) \]
ここで、\( \small \bar{p} \)は運動量、\( \small \sigma \)は観測される位置の不確実性を表すパラメータである。このとき、観測される座標の確率分布は正規分布に従っており、
\[ \small P(x,y,0)=|\psi(x,y,0)|^2 = \frac{1}{\sigma\pi} \exp\left(-\frac{x^2+y^2}{\sigma^2}\right) \]
と書くことができる。波動関数の時間発展はSchrödinger方程式
\[ \small i \hbar\frac{\partial \psi(x,y,t)}{\partial t} = – \frac{1}{2} \frac{\hbar^2}{m} \left( \frac{\partial^2 \psi(x,y,t)}{\partial x^2} + \frac{\partial^2 \psi(x,y,t)}{\partial y^2} \right) \]
に従わなければならないので、変数分離を適用しそれぞれ時間発展を計算すると、
\[ \begin{align*} & \small \psi(x,y,t) = \psi_x(x,t) \psi_y(y,t) \\ & \small \psi_x(x,t) = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \exp \left(- \frac{\left(x-\frac{\bar{p}}{m}t \right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ & \small \qquad \qquad \times \exp \left(i \left(\frac{\bar{p}}{\hbar} \left(x-\frac{\bar{p}}{m}t \right) + \frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left(x-\frac{\bar{p}}{m}t \right)^2}{2 m \sigma^4 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \right) \\ & \small \psi_y(y,t) = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \exp \left(-\frac{y^2}{2 \sigma^2 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ & \small \qquad \qquad \times \exp \left(i \frac{\hbar t y^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \end{align*} \]
を得る。したがって、
\[ \begin{align*} & \small \psi(x,y,t) = \frac{1}{\pi^{1/2}\sigma} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)} \exp \left(-\frac{\left(x-\frac{\bar{p}}{m}t \right)^2 + y^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ & \small \qquad \qquad \times \exp \left(i \left( \frac{\bar{p}}{\hbar} \left( x – \frac{\bar{p}}{m}t \right) + \frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left( \left(x-\frac{\bar{p}}{m}t \right)^2 + y^2 \right)}{2 m \sigma^4 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \right) \end{align*} \]
及び、
\[ \small P(x,y,t) = |\psi(x,y,t)|^2 = \frac{1}{\pi \sigma \left( 1+\left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)^{1/2}} \exp \left(- \frac{\left(x-\frac{\bar{p}}{m}t \right)^2 + y^2}{\sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \]
が成り立つ。上記の確率分布は運動量が一定値の場合に観測される位置が従う確率分布であるが、アンサンブルで記述する場合、その速度が正規分布に従うかのような確率分布になっている。すなわち、量子の運動量が一定(0の場合でも)であっても、それを表現するアンサンブルの運動量は一定値とならず確率的な変動をすることになる。したがって、量子の運動量\( \small \bar{p} \)とアンサンブルの運動量\( \small p \)の差を確率的なモデルで表す必要がある。
量子の観測確率分布と回折のような事象との整合性を考えると、アンサンブルの運動量\( \small p \)の確率過程はガウス型のホワイトノイズ過程と考えられるが、連続時間のホワイトノイズ過程は数学的に取り扱うことが難しい(分散が0であるが0ではない値をとる二重数のような仮想的な確率過程を考える必要がある。)。金融での応用では連続時間であることはさほど重要ではないので(興味のある読者はAppendix参照。)、時間を離散化してモデルを表現する。この確率分布を満たす確率過程をリバースエンジニアリングで推定した場合、次の確率過程が有力であると考えられる。\( \small x,y \)をアンサンブルの位置、\( \small \bar{x}, \bar{y} \)を内部の状態としてのアンサンブルの位置、\( \small p_x, p_y \)をアンサンブルの運動量、時間間隔を\( \small \Delta t\)とすると、
\[ \begin{align*} & \small \bar{x}(t) = \bar{x}(t-\Delta t) + \frac{p_x(t-\Delta t)}{m} \Delta t, \quad \bar{x}(0) = 0 \\ & \small \bar{y}(t) = \bar{y}(t-\Delta t) + \frac{p_y(t-\Delta t)}{m} \Delta t, \quad \bar{y}(0) = 0 \\ & \small p_x(t) = \bar{p} + \sqrt{\frac{\hbar^2}{2\sigma^2}}\epsilon_x(t) \\ & \small p_y(t) = \sqrt{\frac{\hbar^2}{2\sigma^2}}\epsilon_y(t) \\ & \small x(t) = \bar{x}(t) + \sqrt{\frac{\sigma^2}{2}}\eta_x(t) \\ & \small y(t) = \bar{y}(t) + \sqrt{\frac{\sigma^2}{2}}\eta_y(t) \\ & \small \left(\epsilon_x(t), \epsilon_y(t), \eta_x(t), \eta_y(t)\right) \sim N_4(0, 1) \end{align*} \]
が上記のモデルと平均と分散が一致する時系列モデルと考えられる。内部状態としての初期位置は原点に固定されているが、これは最初の内部状態としての位置を原点とみなすだけであり、一般性を失うことはないことに注意する。ここで \( \small N_4 (0, 1) \)は4次元標準正規分布であり、最初の4本の方程式と運動量\( \small \bar{p} \)を状態方程式、残りの2本を観測方程式とした状態空間モデルである。Feynmanは経路積分を状態空間モデルとして記述しなかったが、本質的には経路積分と等価のアプローチと考えることができる。
最後に、上記のモデルが持つ直感的な物理的解釈を示す。モデルが何を表現しているかを知る最も効率的な方法は、二重スリット実験をどう考えるかを示すことだろう。モデルの二重スリット実験の解釈は次のとおりである。
- 一個の量子を空間に広がる確率分布(アンサンブル全体の分布)とその確率分布からサンプリングされる観測値(一つのアンサンブル)の組み合わせと考える。
- 二重スリットの実験では、量子の観測確率分布(アンサンブル全体の分布)は同時に2つのスリットを通過する。
- 観測される座標は各観測時点でアンサンブルの中からランダムにサンプリングされるので、連続的な経路を持たず、どちらのスリットを通過したかという情報を持たない。
適切ではないかもしれないが(アンサンブル間の干渉を処理するには、位相の情報を別途処理する必要がある。)、状態空間モデルでの量子の確率分布(アンサンブル)のモンテカルロシミュレーションの視覚的イメージは次のとおりである。
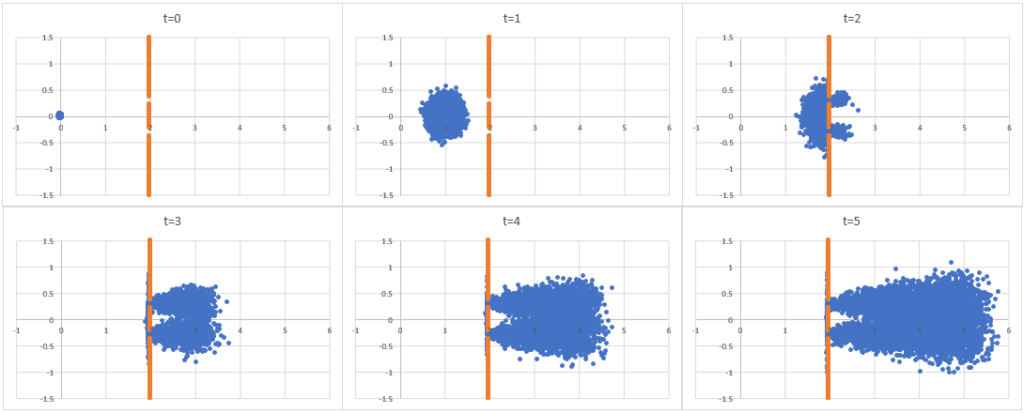
波束モデル
量子力学の確率分布は波動の性質を持っているので、離散時間のホワイトノイズとして扱うよりも、フーリエ変換を実行して三角関数のモデルに変換する方がよいだろう。離散時間のホワイトノイズ過程は、離散フーリエ変換を適用することにより、ガウス型波束モデルに変換できる。フーリエ変換に馴染みがない読者は、座標軸としての時間を三角関数の組み合わせに変換し、スプライン補間のように連立方程式で同じ点を通過するように変換したものと考えれば簡単に理解できるだろう。
\( \small p_0,p_1,\cdots,p_{n-1}, p_j = p(j\Delta t) \)を\( \small n \)個(\( \small n \)は偶数とする。)の時間グリッドで区切った一つの軸のアンサンブルの運動量のサンプルパスとする。このとき、離散フーリエ変換とその逆変換は、
\[ \begin{align*} & \small P_j = \sum_{t=0}^{n-1} p_t \exp \left(-2\pi t \frac{j}{n\Delta t}i \right) \\ & \small p_t = \frac{1}{n} \sum_{j=0}^{n-1} P_j \exp \left(2\pi t \frac{j}{n\Delta t}i \right) \end{align*} \]
であり、フーリエ係数の実部と虚部は、
\[ \begin{align*} & \small a_j = \Re[P_j] = \sum_{t=0}^{n-1} p_t \cos \left(-2\pi j \frac{t}{n\Delta t}\right) \\ & \small b_j = \Im[P_j] = \sum_{t=0}^{n-1} p_t \sin \left(-2\pi j \frac{t}{n\Delta t}\right) \end{align*} \]
で与えられる。\( \small p_t \)は分散\( \small \hbar^2/2\sigma^2 \)の独立な正規分布に従っているので、フーリエ係数\(\small a_0\)、および、\( \small a_j,b_j,j>0 \)もそれぞれ正規分布\( \small a_0 \sim N(n\bar{p},n\hbar^2/2 \sigma^2) \)、\( \small a_j,b_j \sim N (0, n\hbar^2/4 \sigma^2) \)に従う。ここで、\( \small b_0=0 \)であり、これらは三角関数がそれぞれ直交し、かつ、二乗の期待値が
\[ \small \frac{1}{n}\sum_{t=0}^{n-1} \cos \left(-2\pi j \frac{t}{n\Delta t}\right)^2 \approx \frac{1}{n} \sum_{t=0}^{n-1} \sin \left(-2\pi j \frac{t}{n\Delta t}\right)^2 \approx \frac{1}{2} \]
であることから計算できる。したがって、基底関数\( \small \phi_j(t) \)を
\[ \small \left[ \begin{array}{c} \phi_0(t) \\ \phi_1(t) \\ \vdots \\ \phi_{n/2}(t) \\ \phi_{n/2+1}(t) \\ \vdots \\ \phi_{n-1}(t) \ \end{array} \right] = \left[ \begin{array}{c} 1 \\ \cos \left(2\pi t \frac{1}{n\Delta t}\right) \\ \vdots \\ \cos \left(2\pi t \frac{n/2}{n\Delta t}\right) \\ \sin \left(2\pi t \frac{1}{n\Delta t}\right) \\ \vdots \\ \sin \left(2\pi t \frac{n/2-1}{n\Delta t}\right) \ \end{array} \right] \]
と定義し、元のデータをフーリエ係数を使って再現すれば、
\[ \begin{align*} & \small p_t = \frac{2}{n} \left(\frac{a_0}{2} + \sum_{j=1}^{n/2-1} a_j \phi_j(t) + \sum_{j=1}^{n/2-1} b_j \phi_{n/2+j}(t) + a_{n/2} \phi_{n/2} (t) \right) \\ & \small \quad = \frac{\hbar}{n} \sum_{j=0}^{n-1} k_j \phi_j(t) = \hbar k(t), \; k_0 \sim N \left(\frac{n\bar{p}}{\hbar}, \frac{n}{2\sigma^2}\right), \; k_j \sim N \left(0, \frac{n}{\sigma^2} \right) \; j > 0 \end{align*} \]
を得る。ここで、\( \small k(t) = 1/n\sum_{j=0}^{n-1} k_j \phi_j(t) \sim N(\bar{p}/\hbar, 1/2\sigma^2) \)は波数(wavenumber) といわれる値であり、波数が正規分布に従うモデルがガウス型波束モデルということになる。波数の分散を\( \small \sigma_k^2 = 1/2\sigma^2 = 1/4\sigma_x^2 \)とすれば、波束に関する不確定性原理\( \small \sigma_x\sigma_k \geq 1/2 \)を得ることができる。アンサンブルの運動量を直接シミュレーションする代わりにアンサンブルの波数をシミュレーションしても等価な結果を得ることができる。
アンサンブルの座標に関する状態方程式で運動量を上記の式で置き換えれば、最終的な量子の状態空間モデル
\[ \begin{align*} & \small \bar{x}(t) = \bar{x}(t-\Delta t) + \frac{\hbar\Delta t}{mn}\sum_{j=0}^{n-1} k_j \phi_j(t) \\ & \small x(t) = \bar{x}(t) + \epsilon(t), \quad \epsilon(t) \sim N \left(0, \frac{\sigma^2}{2}\right) \end{align*} \]
を得ることができる。これは\( \small \Delta t = 1 \)とおいてパラメータをまとめれば、最初に提案した時系列モデルと同じ形式であった。
運動量とポテンシャル
波束モデルを使用するメリットを示す。 物理学では、一般に粒子の運動をポテンシャルと運動量の情報を外生的に与えて記述する。 一方で、金融市場ではそのような情報を観測することができず、運動量やポテンシャルは外生的に与えられない状況のモデルを考える必要がある。このような状況においても、観測される市場データを用いて波数が従う分布と値を推定すれば、間接的にポテンシャルと運動量の情報を推定することができる。波数の情報が運動量とポテンシャルの情報と同等であることを示すことで理解できるだろう。視覚的なイメージは以下の図のとおりであり、波数モデルがトレンドラインを利用したテクニカル分析と類似のモデルであることがわかるだろう。
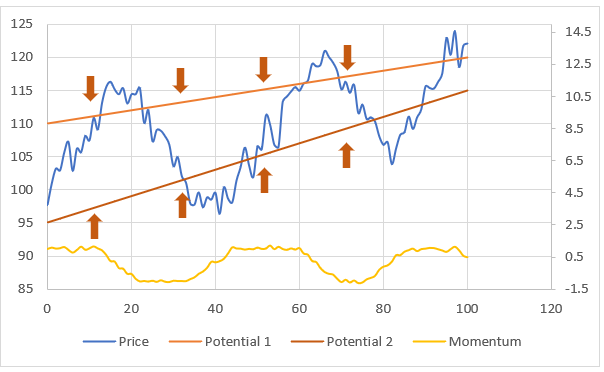
簡略化のため1次元のモデルを用いて、波数、運動量、ポテンシャルの関係を位相における関係から説明する。アンサンブルの運動量のシミュレーションパス\( \small p^{(d)}(t)\)( \( \small (d)\) で番号付けする。)から逆算された波数を\( \small k^{(d)}(t) \)と表す。時点0における波動関数の複素数部分(Feynman核)は、
\[ \small K^{(d)}(0) = \exp \left(i k^{(d)}(0) \bar{x}^{(d)}(0) \right) \]
であり、波数の時間に関する微分値が0で近似できるとすると、Schrödinger方程式から
\[ \begin{align*} & \small K^{(d)}(t) = \exp\left(i k^{(d)}(t) \bar{x}^{(d)}(t) – i \frac{\hbar}{2m} \int_0^t k^{(d)}(s)^2 ds\right) \\ & \small \qquad \quad \approx \exp\left(\frac{i}{\hbar} \left(p^{(d)}(t) \bar{x}^{(d)}(t) – \frac{1}{2m} \int_0^t p^{(d)}(s)^2 ds\right)\right) \end{align*} \]
を得る。ポテンシャル関数\( \small V(x,t) \)がある場合の運動量の経路は
\[ \small p^{(d)}(t) \approx p^{(d)}(s)-\int_s^t \frac{\partial V(\bar{x}^{(d)}(u),u)}{\partial x} ds \]
で近似できるので、
\[ \small p^{(d)}(t) \bar{x}^{(d)}(t) \approx \frac{1}{m} \int_0^t p^{(d)}(s)^2 ds-\int_0^t \frac{p^{(d)}(s)}{m} \int_s^t \frac{\partial V(\bar{x}^{(d)}(u),u)}{\partial x} duds \]
を得る。\( \small p(s)/m = d\bar{x}(s)/ds \)であるから積分の順序を交換すれば
\[ \begin{align*} & \small p^{(d)}(t) \bar{x}^{(d)}(t) \approx \frac{1}{m} \int_0^t p^{(d)}(s)^2 ds-\int_0^t \int_0^s \frac{\partial V(\bar{x}^{(d)}(u),u)}{\partial x} d\bar{x}^{(d)}(u)ds \\ & \small \qquad \qquad \;\;\; = \frac{1}{m} \int_0^t p^{(d)}(s)^2 ds-\int_0^t V(\bar{x}^{(d)}(s), s) ds \end{align*}\]
となり、最終的に
\[ \small K^{(d)}(t) = \exp\left(\frac{i}{\hbar} \left(\frac{1}{2m} \int_0^t p^{(d)}(s)^2 ds-\int_0^t V(\bar{x}^{(d)}(s), s) ds \right)\right) \]
が成り立つ。
すなわち、アンサンブルの現在の座標と波数に関する情報は、アンサンブルの運動量とポテンシャルに関する情報と等しいことがわかる。\( \small K(x, t) = E[K^{(d)}(t) | \bar{x}(t) = x] \)と定義すれば、これはFeynmanの経路積分と等価である。相当の工夫は要求されるだろうが、この条件付き期待値は格子状のシミュレーションや最小二乗モンテカルロ法 (Longstaff and Schwartz (2001)参照。)で推定できるかもしれない。
結論と今後の方向性
本稿では、リバースエンジニアリングによりSchrödinger方程式から導出される時系列モデル(波束モデル)を紹介し、金融時系列モデルへの適用の可能性を示した。このアプローチは金融市場におけるテクニカル分析の一般化と考えることができる。具体的な波数の値や分布推定の方法については記述していないが、状態空間モデルの様々な推定方法が適用できると考えられる。特に内部パラメータ(本稿における波数)を内部の状態として扱うを扱うモデルを自己組織化モデルといい、観測データの変化に応じてモデルを適応させるアプローチをデータ同化という。データ同化を用いたモデルの構築方法は別の機会に紹介したいと考える。
参考文献
[1] Feynman, Richard. P. and Albert. R. Hibbs. Quantum Mechanics and Path Integrals. McGraw-Hill, 1965.
[2] Longstaff, Francis. A. and Edward. S. Schwartz. Valuing American options by simulations : A simple least – squares approach. Review of Financial Studies, 14:113―147, 2001.
[3] Nelson, Edward. Quantum Fluctuations. Princeton University Press, 1985.
[4] Tomonaga, Shin-ichiro. Quantum Mechanics Volume 1:Old Quantum Theory. North-Holland., 1962.
[5] Tomonaga, Shin-ichiro. Quantum Mechanics Volume 2:New Quantum Theory. John Wiley & Sons (Interscience Publishing), 1966.
Appendix. 連続時間のホワイトノイズ過程
本文では、連続時間のホワイトノイズ過程の時間に関する積分が\( \small N(0, \sigma^2 t^2) \)に従うということを天下り的に導入したが、これは直感的な計算とは明らかに乖離している結論に見える。素直に計算すれば、時間グリッドを細かくするにつれて大数の法則で0に収束すると考えられるし、分散を調整して離散時間で計算する(時間を分割して1グリッドあたりの乱数の分散を\( \small 1/dt \)で基準化して計算する。)と、これは\( \small N(0, \sigma^2 t) \)であり標準ブラウン運動となる。具体的には\( \small \Delta t = t/n \)、連続時間のホワイトノイズ過程を\( \small W(t) \)、離散時間のホワイトノイズを\( \small w_j \)とおくと
\[ \begin{align*} & \small \int_0^t W(s) ds \approx \sum_{j=1}^n w_j \Delta t \sim N\left(0, \frac{\sigma^2t^2}{n} \rightarrow 0 (n \rightarrow \infty)\right), w_j\sim N(0,\sigma^2) \\ & \small \int_0^t W(s) ds \approx \sum_{j=1}^n w_j \Delta t \sim N\left(0, \sigma^2t\right), w_j\sim N\left(0,\frac{\sigma^2}{\Delta t}\right) \end{align*} \]
である。そのため、確率解析では連続時間のホワイトノイズ過程はブラウン運動の時間に関する微分として定義することが一般的である。しかしながら、これは無限次元の計算結果が有限次元の直感的な計算結果と乖離する稀によくある(?)事例のように見える。
具体的に、連続時間のホワイトノイズ過程を平均と分散が0であるにもかかわらず0ではない値をとる二重数のような仮想的な確率過程\( \small \nu(t) \)が存在するものと仮定して定義すると以下のようになる。連続時間のホワイトノイズ過程は\( \small \nu(t) \)を用いて
\[ \small \nu(t)dt = dW(t), \quad W(t) \sim N(0, \sigma^2),\; \forall t \]
となる。積分の形で表せば
\[ \small W(t) = W(0) + \int_0^t \nu(s) ds \]
であり、\( \small W(t) \)を時間について積分すると、
\[ \small X(t) = \int_0^t W(s) ds = W(0)t + \int_0^t \int_0^s \nu(u) duds \]
となる。\( \small X(t) \)の分散を計算すると第2項は無視できるので\( \small \sigma^2t^2 \)となる。当然のことながら、\( \small \nu(t) \)のような確率過程は実数空間には存在しないため、離散時間のホワイトノイズ過程の極限として連続時間のホワイトノイズ過程を定義することができないことになる。この類の無限次元に関する取扱いの難しさが量子力学やSchrödinger方程式を確率解析で理解することを困難にしている原因と考えられる。



コメント