一次元クーロンポテンシャルのシュレディンガー方程式

問題設定

　一次元のクーロンポテンシャル

\[ \small E = \frac{p^2}{2m}+e^2|x| \]

を考える。一次元の場合に、ポテンシャル関数がどのようなものになるか現実には不明であるが、次元が\(\small D\)である場合

\[ \small V(r) = -\frac{e^2}{r^{D-2}} \]

であると仮定しよう（\(\small D=1\)の場合は符号が反対になる。）。１次元のクーロンポテンシャルが座標の差に比例する関数になるということは、例えばDirac(1932)などにより一定の支持が与えられているだろう（係数として\(\small 2\pi\)が掛かるみたいだが、ここでは省略する。）。量子力学における対応原理から導出したシュレディンガー方程式

\[ \small i\hbar\frac{\partial\psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x,t)}{\partial x^2}+e^2|x|\psi(x,t) \]

の解を求めよう。この形式の方程式を直接解くのは難しいので、一次元の重力同様に\(\small x>0\)、\(\small x<0\)で領域を分けて

\[ \small \begin{align*} &i\hbar\frac{\partial\psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x,t)}{\partial x^2}+e^2x\psi(x,t), \quad x>0 \\
&i\hbar\frac{\partial\psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x,t)}{\partial x^2}-e^2x\psi(x,t), \quad x<0 \end{align*} \]

と考えることにする。この問題はしばしば三角井戸型ポテンシャルといわれる問題で、エアリー関数（Airy Function）を用いて解く問題であるらしい。しかし、基底関数を求めても具体的な確率分布は想像しがたいので、ここでは簡便的な近似を用いて解の形式を推測してみる。

　\(\small t=0\)において\(\small x>0\)であると仮定し、その時点における座標の期待値を\(\small x_0\)、運動量の期待値を\(\small p_0\)とおく。近似的な仮定として座標の不確定性が正規分布に従うと仮定して、初期時点の波動関数が

\[ \small \psi(x, 0) = \psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{(x-x_0)^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} p_0 (x-x_0) \right) \]

であると仮定する。これが近似的であるのは、\(\small x<0\)についても確率を持ってしまうためである。\(\small \sigma\)​が十分に小さい値であると仮定し、そういった確率は無視できるものとする。以上のことから、解くべき問題の基礎方程式と境界条件は

\[ \small \begin{align*} &i\hbar\frac{\partial\psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x,t)}{\partial x^2}+e^2x\psi(x,t), \quad x > 0 \\ &\psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{(x-x_0)^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} p_0 (x-x_0) \right) \end{align*} \]

であり、このときの\(\small \psi(x,t)\)を求めよ、ということになる。若干インチキ臭い方法であるが、近似的に解を求めてみよう。

近似解の導出

　境界条件をフーリエ変換して

\[ \small \psi(x,0) = \int_{-\infty}^\infty A_k\exp(ikx) dk \]

と置く。逆フーリエ変換から振幅を計算すると

\[ \small A_k = \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}}\exp\left(-\frac{\sigma^2}{2}\left(\frac{p_0}{\hbar}-k\right)^2\right) \]

となるのであった。\(\small \psi_k(x, t) = A_k\exp(ikx-i\omega t)\)と仮定すれば

\[ \small \frac{\partial \psi_k(x,t)}{\partial x} = ik\psi_k(x,t) \]

であるから、

\[ \small \frac{\partial^2 \psi_k(x,t)}{\partial x^2} = -k^2\psi_k(x,t) \]

が成り立つ。シュレディンガー方程式に代入すれば

\[ \small \frac{\partial \psi_k(x,t)}{\partial t} = -\left(i\frac{\hbar k^2}{2m}-i\frac{e^2}{\hbar}x\right)\psi_k(x,t) \]

を得る。

\[ \small \frac{\partial \ln \psi_k(x,t)}{\partial t} = \frac{1}{\psi_k(x,t)}\frac{\partial \psi_k(x,t)}{\partial t} \]

であるから、時間について積分すれば

\[ \small \ln \psi_k(x,t) = -i\frac{\hbar k^2}{2m}t+i\frac{e^2}{\hbar}\int_0^tx(u)du+C \]

\(\small t=0\)のとき境界条件を満たすように積分定数\(\small C\)を定めれば

\[ \small \psi_k(x,t) = \exp\left(ik(x-x_0)-i\frac{\hbar k^2}{2m}t+i\frac{e^2}{\hbar}\int_0^tx(u)du \right) \]

を得る（符号が反対っぽいが気にしないことにする）。

　\(\small x\)の時間に関する積分をどのように定めれば良いかという問題が生じるが、古典力学的な近似から平均的には

\[ \small x(u) \approx x_0+\frac{p_0}{m}u-\frac{1}{2}\frac{e^2}{m}u^2 \]

と推測することができるだろう。加速度は\(\small ma=-e^2\)から計算している。積分を計算すれば

\[ \small \int_0^tx(u)du = x_0t+\frac{p_0}{2m}t^2-\frac{1}{6}\frac{e^2}{m}t^3 \]

となる。波動関数の基底関数に代入すると

\[ \small \psi_k(x,t) = \exp\left(ik(x-x_0)-i\frac{\hbar k^2}{2m}t+i\frac{e^2}{\hbar}x_0t+ik\frac{e^2}{2m}t^2-i\frac{e^4}{6m\hbar}t^3 \right) \]

と表すことができる。したがって、波動関数は

\[ \small \begin{align*} \psi(x,t) = & \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}} \\ & \times \int_{-\infty}^\infty \exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2+ik(x-x_0)-i\frac{\hbar k^2}{2m}t+i\frac{e^2}{\hbar}x_0t+ik\frac{e^2}{2m}t^2-i\frac{e^4}{6m\hbar}t^3 \right) dk \end{align*} \]

を計算すればよい。めんどくさそうに見えるが実をいうと、自由粒子の解

\[ \small \begin{align*} \psi(x,t) \; & = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left( x-\frac{\bar{p}}{m}t \right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{\hbar}x – \frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left( x-\frac{\bar{p}}{m}t \right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right) \ \end{align*} \]

において、\(\small x\)を\(\small x-x_0+e^2t^2/2m\)に置き換えて、

\[ \small \exp\left(i\frac{e^2}{\hbar}x_0t-i\frac{e^4}{6m\hbar}t^3\right) \]

を掛ければ、解になることは確認できるだろう。これらの項は\(\small k\)に依存しないので積分の外に出せるためである。まとめると

\[ \small \begin{align*} \psi(x,t) \; & = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left( x-x_0-\frac{p_0}{m}t +\frac{1}{2}\frac{e^2}{m}t^2\right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{p_0}{\hbar}x – \frac{p_0^2 t}{2m \hbar}+\frac{e^2}{\hbar}x_0t +\frac{p_0e^2}{2m\hbar}t^2-\frac{e^4}{6m\hbar}t^3+ \frac{\hbar t \left( x-x_0-\frac{p_0}{m}t+\frac{1}{2}\frac{e^2}{m}t^2 \right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right) \ \end{align*} \]

を得ることができる。この解が満たす偏微分方程式は

\[ \small i\hbar\frac{\partial\psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x,t)}{\partial x^2}+e^2\left(x_0+\frac{p_0}{m}t-\frac{1}{2}\frac{e^2}{m}t^2 \right)\psi(x,t) \]

であり、元の基礎方程式と異なるが

\[ \small x = x_0+\frac{p_0}{m}t-\frac{1}{2}\frac{e^2}{m}t^2 \]

と置き換えれば、両者が近似的には一致することが確認できるだろう。\(\small x<0\)の場合は加速度の項の符号が反対になるだけである。

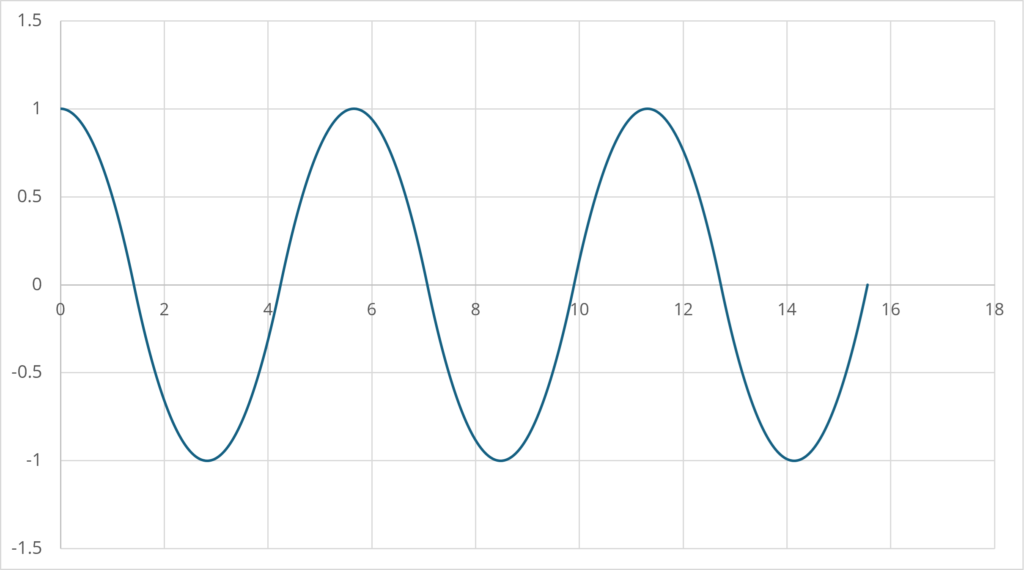
　以上のことから、１次元の重力で考察したように周期的な運動に量子力学的な不確定性の項を追加した運動（以下のグラフに正規分布のノイズを足したもの）が１次元のクーロンポテンシャルに束縛された電子の運動であると推測できる。

定常状態は虚構に過ぎない？

　おそらく、ここまで読んだ読者の中には、そんな近似解ではなくて定常状態における確率分布（\(\small t\)に依存しない解）を計算しろよ、と思った人もいるかもしれない。しかし、現実には量子は確率的な運動をしていると考えられるため、実をいうとそれぞれの時点時点では同じ検出確率分布を厳密には持っていないと推測できる。短い時間単位では確率分布は推移しているがその時間間隔があまりに短いために、あたかも確率分布が定常である（時間変化していない）ように我々は錯覚しているのだろう。定常状態でなければ、安定的な状態にならないと思うかもしれないが、上記の解のような周期解では定常でなくても一定の安定性を持った運動をすることになると考えられる。このように考えると、定常状態における解というのは我々人間が考えるモデルであって、現実の量子がそのような状態を取っていることはないのかもしれない、ということに注意が必要だろう。

　例えば、上記の例で周期的な運動が非常に速いために一周期のいずれの時点で検出されるか区別することができない場合を考える。この場合、

\[ \small \begin{align*} &x(t)=a-\frac{1}{2}\frac{e^2}{m}t^2, \quad x\in[0,a] \\ &x(t)=-a+\frac{1}{2}\frac{e^2}{m}t^2, \quad x\in[-a, 0] \ \end{align*} \]

において、いずれの時点\(\small t\)で検出されるか定めることができないということになる。もし、\(\small t\)が一様分布に従う確率変数であると仮定すると、定義域は

\[ \small t \in \left[0, \sqrt{\frac{2ma}{e^2}}\right] \]

であるから、\(\small t\)の確率密度関数は

\[ \small p(t) = \sqrt{\frac{e^2}{2ma}} \]

となる。\(\small x(t)\)の逆関数を計算すると

\[ \small t(x) = \sqrt{\frac{2m}{e^2}(a-x)} \]

であるから、\(\small x>0\)における\(\small x(t)\)の確率密度関数は

\[ \small p(x) =　\frac{\sqrt{\frac{e^2}{2ma}}\frac{dt(x)}{dx}}{\int_0^a\sqrt{\frac{e^2}{2ma}}\frac{dt(x)}{dx}dx} = \frac{1}{2\sqrt{a(a-x)}}, \quad x \in[0,a] \]

と計算できる。\(\small x>0\)と\(\small x<0\)で確率分布は対称であるから

\[ \small p(x) = \frac{1}{4\sqrt{a(a-|x|)}}, \quad x \in [-a,a] \]

が確率密度関数になるだろう。これに量子力学的なノイズを加えた確率分布が定常状態における確率分布ということになるかもしれない。しかし、この確率分布はおそらく1次元クーロンポテンシャルのシュレディンガー方程式を満たす波動関数から導出することは困難であるだろう。言い換えれば、定常状態のシュレディンガー方程式の解は電子の検出確率分布を適切に導出しないケースがあるかもしれないということになる。適切な検出確率分布を導出するためには時間依存のシュレディンガー方程式を解いたうえで、上記のように時間について平均化した確率分布を計算するという手続きを踏まなければならないかもしれない。

おまけ：エアリー関数

　エアリー関数は

\[ \small \begin{align*} &\text{Ai}(x) = \frac{1}{\pi}\int_0^\infty \cos\left(\frac{t^3}{3}+xt \right)dt \\ &\text{Bi}(x) = \frac{1}{\pi}\int_0^\infty \exp\left(-\frac{t^3}{3}+xt \right)+\sin\left(\frac{t^3}{3}+xt \right)dt \end{align*} \]

で定義される関数で、微分方程式

\[ \small \frac{d^2f(x)}{d^2x}-xf(x) =0 \]

の解である。1次元クーロンポテンシャルのシュレディンガー方程式

\[ \small i\hbar\frac{\partial\psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x,t)}{\partial x^2}+e^2x\psi(x,t) \]

は

\[ \small \psi(x,t) = \Psi(x)\exp\left(-i\frac{E}{\hbar}t \right) \]

と置けば

\[ \small E\Psi(x) =-\frac{\hbar^2}{2m}\frac{d^2\Psi(x)}{dx^2}+e^2x\Psi(x) \]

と表すことができる。したがって、

\[ \small \frac{d^2\Psi(x)}{dx^2}+\frac{2me^2}{\hbar^2}\left(\frac{E}{e^2}-x\right)\Psi(x)=0 \]

と変形できる。

\[ \small \xi =-\left(\frac{E}{e^2}-x \right)\left(\frac{\hbar^2}{2me^2}\right)^{-\frac{1}{3}} \]

と変数変換すれば

\[ \small \frac{d^2\Psi(\xi)}{d\xi^2}-\xi\Psi(\xi)=0 \]

となり、エアリー関数の微分方程式を得ることができる。したがって、

\[ \small \Psi(\xi) = c_1\text{Ai}(\xi)+c_2\text{Bi}(\xi) \]

の形式で解を求めることができて、エアリー関数を基底とする線形結合の関数で波動関数を表すことができる。ただし、エネルギーの値は固有値問題として解を求めなければならないし、おそらく解析的に波動関数を求めることはできないと思われる。

　本稿で導出した近似解とエアリー関数で何の関係もないように思えるかもしれない。しかし、３変数のエルミート多項式のテーラー展開を考えると

\[ \small \exp\left(xt+yt^2+zt^3 \right) = \sum_{n=0}^\infty {}_3H_n(x,y,z) \frac{t^n}{n!} \]

と表すことができるらしく、この３変数のエルミート多項式はGauss-Airy関数（記号が紛らわしいが、\(\small y,z\)は定数である。\(\small y=0,z=-1/3\)と置けばエアリー関数になることが確認できるだろう。）

\[ \small \text{GAi}(x,y,z) = \frac{1}{\pi}\int_0^\infty e^{-yt^2}\cos\left(xt-zt^3\right)dt \]

を用いて

\[ \small {}_3 H_n(x,y,z) = \int_{-\infty}^\infty \xi^n\text{GAi}(\xi-x,y,z)d\xi \]

と表すことができるらしい。うまく式を変形すれば、この形式に持ち込むことができて、\(\small t\)に関する三次関数として計算する本稿の計算に一定の妥当性を与えられそうな気がするが・・・まあ、無理そうなのでやめておこう。

参考文献

[1] Dirac, Paul.A.M (1932), Relativistic Quantum Mechanics. Proceedings of the Royal Society A, 136, 453-464.