1次元空間の重力
空間が1次元(時空が2次元)の場合の重力を考察する。空間が1次元である場合に重力について逆二乗則が成り立つかという疑問が生じるが、これは空間が\(\small D\)次元である場合
\[ \small \frac{d^2x}{dt^2} = -\frac{GM}{r^{D-1}}\frac{x}{r} \]
であると考えた方が適切だろう。重力について逆二乗則が成り立つということは空間が3次元であることの根拠として主張されることもある。実際に、特定の座標軸方向に落下する自由落下の問題は1次元空間における重力の問題と同一視することができる。したがって、本稿ではこの式の方を採用し、1次元における重力は
\[ \small \frac{d^2x}{dt^2} = -GM\frac{x}{r} = -GM\frac{x}{|x|} \]
という加速度をもたらす現象と解釈して運動方程式を特定しよう。
相対論的な取り扱いは無視して、古典力学における運動方程式を特定しよう。この場合、ポテンシャル関数は
\[ \small V = mx\frac{d^2x}{dt^2} = -GmM\frac{x^2}{|x|} = -GmM|x| \]
で与えられる。したがって、エネルギーは
\[ \small E = \frac{p^2}{2m}-GmM|x| \]
である。簡便のため、自由落下の運動方程式に合わせて\(\small g=GM\)と表すことにする。(ポテンシャルの符号が反対な気もするが、ポテンシャルが絶対値だと符号を定めることができないように思える。3次元の場合に合わせて負の符号を採用しておく。)
方程式を解くのが難しいように思えるかもしれないが、原点方向に一定の加速度\(\small GM\)で加速する運動であるから、\(\small x>0\)と\(\small x<0\)で分けて積分すればよいだろう。初期点を\(\small x_0\)で速度\(\small dx(0)/dt = 0\)であると仮定しよう。この場合、エネルギーの式から、
\[ \small x_0 = -\frac{E}{GmM} \]
であることに注意する。最初に\(\small x(t)=0\)になるまでは二次関数であるから
\[ \small x(t) = x_0-\frac{1}{2}gt^2, \quad t \in \left[0, \sqrt{\frac{2x_0}{g}}\right] \]
を得る。\(\small x(t)=0\)であるときの速度は
\[ \small \frac{dx(t)}{dt}\Biggl|_{t=\sqrt{2x_0/g}} = -gt = -\sqrt{2x_0g} \]
である。
この境界条件から\(\small x(t)<0\)である区間の運動方程式を求めよう。
\[ \small \frac{d^2x(t)}{dt^2} = g \]
になるので、
\[ \small \frac{dx}{dt} = gt+C_2 \]
\(\small t=\sqrt{2x_0/g}\)のときに値が\(\small -\sqrt{2x_0g}\)であるから、
\[ \small C_2 = -2\sqrt{2x_0g} \]
である。積分すると
\[ \small x(t) = -2t\sqrt{2x_0g}+\frac{1}{2}gt^2+C_1 \]
であるから、\(\small t=\sqrt{2x_0/g}\)のときに値が0になるように積分定数を定めると
\[ \small x(t) =3x_0-2t\sqrt{2x_0g}+\frac{1}{2}gt^2 \]
を得る。\(\small x(t)<0\)の区間だけについて成り立つ式であったから
\[ \small x(t) =3x_0-2t\sqrt{2x_0g}+\frac{1}{2}gt^2, \quad t \in \left[\sqrt{\frac{2x_0}{g}}, 3\sqrt{\frac{2x_0}{g}}\right] \]
である。同様にして、座標の符号が変わるたびに方程式を組み立てると
\[ \small x(t) =-15x_0+4t\sqrt{2x_0g}-\frac{1}{2}gt^2, \quad t \in \left[3\sqrt{\frac{2x_0}{g}}, 5\sqrt{\frac{2x_0}{g}}\right] \\ \small
x(t) =35x_0-6t\sqrt{2x_0g}+\frac{1}{2}gt^2, \quad t \in \left[5\sqrt{\frac{2x_0}{g}}, 7\sqrt{\frac{2x_0}{g}}\right] \;\;\; \\ \small \vdots \]
を得る。グラフにすると以下のようになる(\(\small x_0=1,g=1\)として計算)。
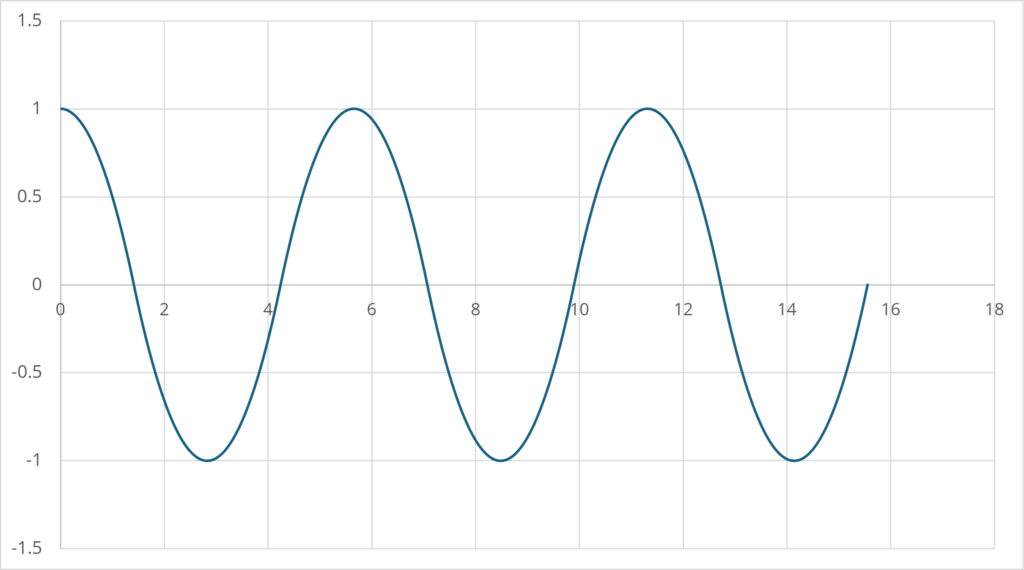
三角関数のように見えるかもしれないが、周期を構成する個々の関数は二次関数であることに注意する。ただし、相当の程度で三角関数で近似することができる。具体的には、時点0で極大値\(\small x_0\)をとり、周期が\(\small T\)である場合
\[ \small x(t) = x_0\cos\frac{2\pi t}{T}=x_0\cos \frac{\pi}{2\sqrt{2}}\sqrt{\frac{g}{x_0}}t \]
と近似できる。周期\(\small T\)は
\[ \small T = 4\sqrt{\frac{2x_0}{g}} \]
であることに注意する。上記の例では
\[ \small x(t) = \cos\frac{\pi}{2\sqrt{2}}t \]
となる。実際に比較すると以下のとおりである。
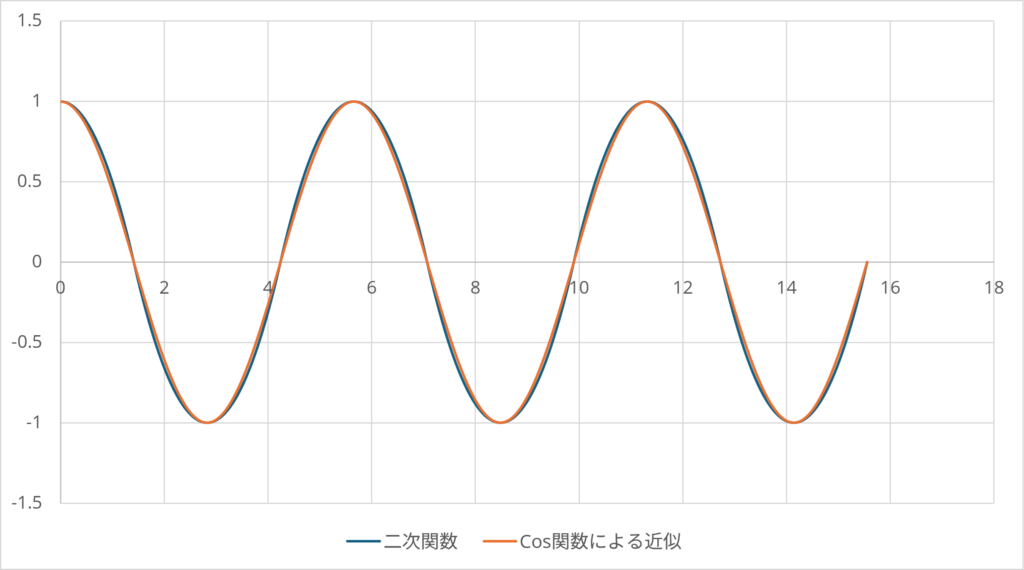
もちろん、原点の質点が大きさを持っていて、運動する物質がそこに着地する場合は原点にとどまることになるだろう。そうでない場合、重力は周期的な運動をもたらす力となると推測される。
1次元空間における二体問題
1次元における重力の運動方程式を求めたが、やはり片方の質点を原点で固定するという操作は適切でないように思える。2つの質点の相対的な運動が上記のようなものであるが、個々の質点はそれぞれ個別の運動をしているものとして記述されるべきだろう。二体問題としてポテンシャル関数を定義すれば
\[ \small V = -Gm_1m_2|x_1-x_2| \]
となるかもしれない。この場合、それぞれの質点の加速度は
\[ \small \begin{align*} &\frac{d^2x_1}{dt^2} = -Gm_2\text{sign}(x_1-x_2) \\ &\frac{d^2x_2}{dt^2} = -Gm_1\text{sign}(x_2-x_1) \end{align*} \]
と計算できる。注意深く計算すれば
\[ \small V=m_1x_1\frac{d^2x_1}{dt^2}+m_2x_2\frac{d^2x_2}{dt^2}=-Gm_1m_2|x_1-x_2| \]
が成り立つことが分かるだろう。積分定数が4つ必要であるから、4つの境界条件を定める必要がある。一般的にしすぎても計算が面倒なので
\[ \small x_1(0) = \frac{x_0}{2},\; x_2(0) = -\frac{x_0}{2},\; \frac{dx_1(0)}{dt} = 0,\; \frac{dx_2(0)}{dt} = 0 \]
で与えられるものとする。一般性を失うことなく、\(\small x_0>0\)と仮定する。このときの運動方程式を特定しよう。
初期時点においては\(\small x_1(t)>x_2(t)\)であるから、加速度は
\[ \small \begin{align*} &\frac{d^2x_1}{dt^2} = -Gm_2 \\ &\frac{d^2x_2}{dt^2} = Gm_1 \ \end{align*} \]
となり、それぞれの式を積分して解を求めればよい。愚直に計算すると
\[ \small \begin{align*} &\frac{dx_1}{dt} = -Gm_2t \\ &\frac{dx_2}{dt} = Gm_1t \ \end{align*} \]
及び、
\[ \small \begin{align*} &x_1(t) = \frac{x_0}{2}-\frac{1}{2}Gm_2t^2 \\ &x_2(t) = -\frac{x_0}{2}+\frac{1}{2}Gm_1t^2 \ \end{align*} \]
と計算できる。\(\small x_1(t)=x_2(t)\)となる\(\small t\)を求めると
\[ \small -\frac{1}{2}G(m_1+m_2)t^2+x_0 = 0 \]
であるから、
\[ \small t = \pm\sqrt{\frac{2x_0}{G(m_1+m_2)}}\]
となる。\(\small t\)はプラスの値を採用する。したがって、
\[ \small \begin{align*} &x_1(t) = \frac{x_0}{2}-\frac{1}{2}Gm_2t^2, \quad t \in \left[0, \sqrt{\frac{2x_0}{G(m_1+m_2)}}\right] \\ &x_2(t) = -\frac{x_0}{2}+\frac{1}{2}Gm_1t^2, \quad t \in \left[0, \sqrt{\frac{2x_0}{G(m_1+m_2)}}\right] \end{align*} \]
を得る。\(\small x_1(t)=x_2(t)\)であるときの速度は
\[ \small \begin{align*} &\frac{dx_1(t)}{dt}\Biggl|_{t=\sqrt{2x_0/G(m_1+m_2)}} = -Gm_2t = -m_2\sqrt{\frac{2x_0G}{m_1+m_2}} \\ &\frac{dx_2(t)}{dt}\Biggl|_{t=\sqrt{2x_0/G(m_1+m_2)}} = Gm_1t = m_1\sqrt{\frac{2x_0G}{m_1+m_2}}
\end{align*} \]
である。
前節同様に、\(\small x_1(t)<x_2(t)\)である区間の運動方程式を計算すると速度は
\[ \small \begin{align*} &\frac{dx_1}{dt} = Gm_2t-2m_2\sqrt{\frac{2x_0G}{m_1+m_2}} \\ &\frac{dx_2}{dt} = -Gm_1t+2m_1\sqrt{\frac{2x_0G}{m_1+m_2}} \end{align*} \]
座標は
\[ \small \begin{align*} &x_1(t) =\left(\frac{1}{2}+\frac{2m_2}{m_1+m_2}\right)x_0-2tm_2\sqrt{\frac{2x_0G}{m_1+m_2}}+\frac{1}{2}Gm_2t^2 \\ &x_2(t) =-\left(\frac{1}{2}+\frac{2m_1}{m_1+m_2}\right)x_0+2tm_1\sqrt{\frac{2x_0G}{m_1+m_2}}-\frac{1}{2}Gm_1t^2 \end{align*} \]
となる。\(\small x_1(t)=x_2(t)\)である\(\small t\)は
\[ \small \begin{align*} &3x_0-2t(m_1+m_2)\sqrt{\frac{2x_0G}{m_1+m_2}}+\frac{1}{2}G(m_1+m_2)t^2=0 \\ \Rightarrow &t = 2\sqrt{\frac{2x_0}{G(m_1+m_2)}}\pm\sqrt{\frac{2x_0}{G(m_1+m_2)}} \end{align*} \]
と計算できる。以上のことから、
\[ \small 2\sqrt{\frac{2x_0}{G(m_1+m_2)}} \]
単位で方程式が切り替わるということが推測できるだろう。前節同様にこれを計算してグラフをつなげると以下のようになる(\(\small m_1=m_2=1/2\)の場合)。
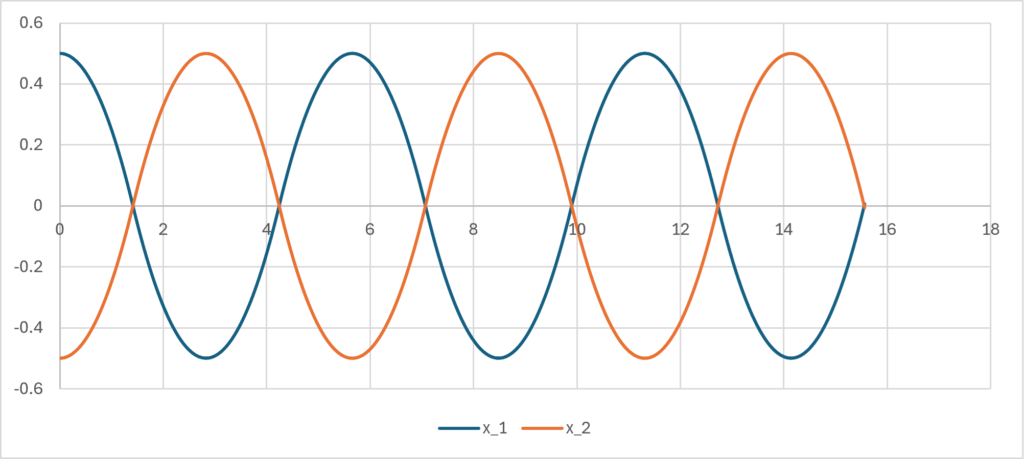
この解は\(\small x_1(t)-x_2(t)\)が前節における\(\small x(t)\)と一致することに注意する。実をいうと、\(\small m_1+m_2=1\)である限り、\(\small x_1(t)-x_2(t)\)の経路は同じ関数になる。例えば、\(\small m_1=0.3,m_2=0.7\)とすると、それぞれの経路は以下のとおりであるが、その差は前節の結果と変わらないということになる。
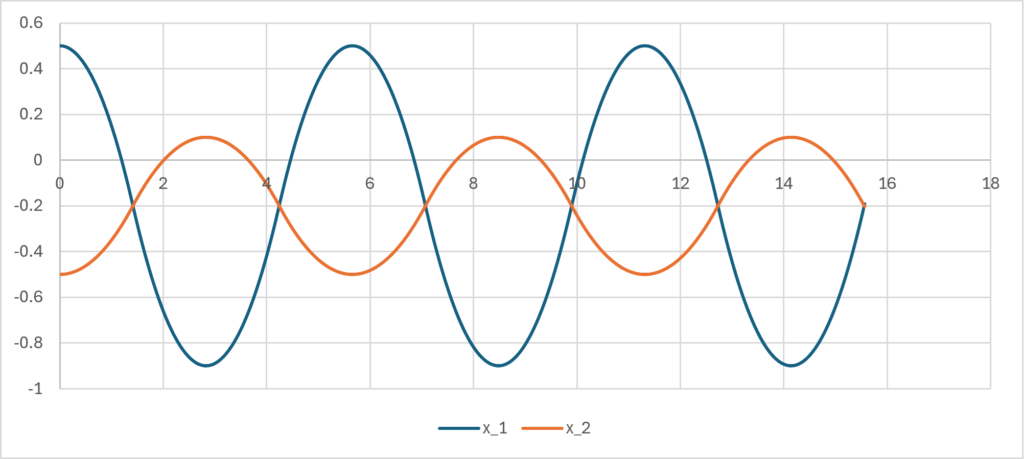
言い換えれば、重力がもたらす距離の運動経路は質量の合算値\(\small m_1+m_2\)のみに依存しており、その構成比率は影響を与えないということである。三角関数で近似すると
\[ \small \begin{align*} &x_1(t) = \frac{x_0}{2}+x_0\frac{m_2}{m_1+m_2}\left[\cos \frac{\pi t}{2\sqrt{2}}\sqrt{\frac{G(m_1+m_2)}{x_0}}-1\right] \\ &x_2(t) = -\frac{x_0}{2}-x_0\frac{m_1}{m_1+m_2}\left[\cos \frac{\pi t}{2\sqrt{2}}\sqrt{\frac{G(m_1+m_2)}{x_0}}-1\right]\ \end{align*} \]
となる。ちなみに、上記で示したグラフはきちんと方程式を解いて計算したのかと思うかもしれないが、ルンゲ・クッタ法で数値的に解いたグラフである。まあ、コンピュータが発達した現代においては真面目に方程式を解く必要性はあまりないということである・・・
まとめと方向性
本稿で扱った内容はあくまでユークリッド空間における引力と考えた場合の運動であり、これを相対論的な時空(円錐座標系)に拡張する必要があるだろう。一般相対性理論では重力を時空を曲げる力として考えているが、円錐座標系(空間が球面であるため、最初から曲がっている)ではどのような影響持つ概念になるかを考察したいということである。3次元で考えるよりは1次元で考えた方がイメージしやすいし、具体的なグラフを描くこともできるということで、これは近いうちに考えてみよう。
考えたい問題は、2つの物質の運動が
\[ \small \begin{align*} &x_1^2+c^2T_{x_1,t}^2 = c^2t^2 \\
&x_2^2+c^2T_{x_2,t}^2 = c^2t^2 \end{align*} \]
で表される場合に、1つの座標系で2つの物質の運動をどのように扱えばよいかということである。おそらく常識外れになるのであるが、2つの3次元球面を足し合わせたものが再び3次元球面になるように合成しなければならない。これは光速で運動する2つの光の速度を合成した値がやはり光速でなければならないという相対論的な性質を満たすようにする必要があることに起因する。これと同じことを質量がある物質、すなわち、光速より遅い物質で考えたらどうなるかということであり、この合成規則の性質が重力というものの本質に関係するのかもしれない。例えば
\[ \small \begin{align*} &E_1^2 = m_1^2c^4+p_1^2c^2 \\ &E_2^2 = m_2^2c^4+p_2^2c^2 \\ &E^2 = (E_1+E_2)^2-2E_1E_2(E_1+E_2)G\frac{|r|}{c^4} \\ &\quad\;\; = E_1^2+E_2^2+2E_1E_2\left(1-\frac{G(E_1+E_2)|r|}{c^4}\right) \end{align*} \]
のようなものであれば
\[ \small E \approx E_1+E_2-G\frac{E_1}{c^2}\frac{E_2}{c^2}|r| \]
となり、古典力学的な近似に一定の正当性を与えることができるようになるかもしれない。計算式の形状から
\[ \small \rho = 1-\frac{G(E_1+E_2)|r|}{c^4} \]
3次元の場合は
\[ \small \rho =1-\frac{G(E_1+E_2)}{c^4r} \]
は何かの相関係数を表しているのかもしれないという仮説を実をいうと筆者は考えている。\(\small \rho \leq 0\)というのがシュワルツシルト解でいうところのブラックホール解に相当しているということになるだろう。球面におけるエネルギーの加算というのは確率変数の加算における分散の計算に類似しているのかもしれない。
加えて、空間の次元を1次元で考察したが、これを2次元にした場合にどうなるか、3次元にした場合にどうなるかと拡張していけば重力の本質にたどり着けるのではないかということである。もちろん、重力がどういったメカニズムで生み出されているかを理解できるわけではないにしても、空間を歪めるといった一般相対性理論におけるアクロバティックな解釈を回避できるようになるかもしれない(重力の影響をすべて時間の性質に押し込めることができるかもしれない)ということで、意味を見出すことができるかもしれない。

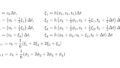

コメント